
一連の観測は、星によって放出される光のスペクトルの作られています。 星のスペクトルの周期的な変化を検出することができ、スペクトル内の特徴的なスペクトル線の波長は一定期間にわたって規則的に増加し、減少する。 その後、統計フィルタがデータセットに適用され、他のソースからのスペクトル効果が相殺されます。 天文学者は、数学的に最適な手法を使用して、軌道上の惑星を示すtell-tale周期的な正弦波を分離することができます。
太陽系外惑星が検出された場合、星の視線速度の変化から惑星の最小質量を決定することができます。 質量のより正確な尺度を見つけるには、惑星の軌道の傾きの知識が必要です。 測定された視線速度と時間のグラフは、特性曲線(円軌道の場合は正弦曲線)を与え、曲線の振幅は、バイナリ質量関数を使用して惑星の最小質量を計算
ベイズ-ケプラー-ピリオドグラムは数学的アルゴリズムであり、それらが周回している星の連続した半径方向速度測定から単一または複数の太陽系外惑星を検出するために使用される。 これは、ケプラー軌道パラメータの一つ以上のセットによって決定された空間上の事前確率分布を使用して、動径速度データのベイズ統計解析を含みます。 この分析は、Markov chain Monte Carlo(MCMC)法を使用して実施することができる。
この方法をHD208487システムに適用し、周期約1000日の第二の惑星を見かけ上検出しました。 しかし、これは恒星活動の人工物である可能性があります。 この方法はHD11964システムにも適用され、約1年の周期を持つ見かけの惑星を発見した。 しかし、この惑星は再縮小されたデータでは発見されず、この検出は太陽の周りの地球の軌道運動の人工物であったことを示唆している。
星の半径方向の速度は惑星の最小質量しか与えませんが、惑星のスペクトル線と星のスペクトル線を区別できれば、惑星自体の半径方向の速度が見られ、これが惑星の軌道の傾きを与えるので、惑星の実際の質量を決定することができます。 このようにして質量を発見した最初の非通過惑星は、スペクトルの赤外線部分で一酸化炭素が検出された2012年のTau Boötis bでした。
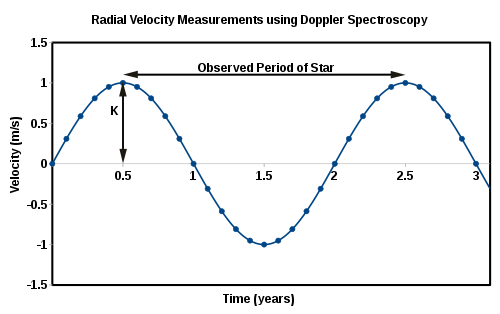
右のグラフは、ドップラー分光法を用いて、惑星によって円軌道で周回されている想像上の星の視線速度を観測する正弦曲線を示しています。 実際の星の観測は同様のグラフを生成しますが、軌道の離心率は曲線を歪め、以下の計算を複雑にします。
この理論的な星の速度は±1m/sの周期的な分散を示しており、この星に重力を引き起こしている軌道質量を示唆しています。 ケプラーの惑星運動の第三法則を用いて、星の周りの惑星の軌道の観測された周期(星のスペクトルの観測された変化の周期に等しい)を使用して、星からの惑星の距離を決定することができる(r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r}

) r3=G M s t a r4≤2p s t a r2{\displaystyle r^{3}={\frac{GM_{\mathrm{star}}}{4\pi^{2}}}P_{\mathrm{star}}}p_{\mathrm{star}}}p_{\mathrm{star}}}p_{\mathrm{star}}}p_{\mathrm{star}}}p_{\mathrm{star}}}p_{\mathrm{star}}{\mathrm{star}}}} }^{2}\,}

どこで:
- rは星からの惑星の距離
- Gは重力定数
- Mstarは星の質量
- Pstarは星の観測周期
r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r{\displaystyle r}}}である。}

, 星の周りの惑星の速度は、ニュートンの重力の法則と軌道方程式を使用して計算することができます: V P L=G M s t a r/r{\displaystyle V_{\mathrm{PL}}={\sqrt{GM_{\mathrm{star}}/r}}{\sqrt{GM_{\mathrm{star}}/r}}}}\,}

ここで、V P L{\displaystyle V_{\mathrm{PL}}}} }}

は惑星の速度である。
計算された惑星の速度から惑星の質量を求めることができます:
M P L=M s t a r V s t a r V P L{\displaystyle M_{\mathrm{PL}}={\frac{M_{\mathrm{star}}V_{\mathrm{star}}}{V_{\mathrm{PL}}}{v_{\mathrm{PL}}}{v_{\mathrm{PL}}}{v_{\mathrm{PL}}}{v_{\mathrm{PL}}}{v_{\mathrm{PL}}}{v_{\mathrm{PL}}}} }}}\,}

ここで、V s t a r{\displaystyle V_{\mathrm{star}}}} }}

は親星の速度である。 観測されたドップラー速度K=V s t a r sin(i){\displaystyle K=V_{\mathrm{star}}\sin(i)}

ここで、iは視線に垂直な線に対する惑星の軌道の傾きです。
したがって、惑星の軌道傾斜角と星の質量の値を仮定すると、観測された星の視線速度の変化を用いて太陽系外惑星の質量を計算することができ