na tej stronie określono transformaty Fouriera dla sinusoidalnych sinusoidalnych i funkcji cosinus. Wynik można łatwo uzyskać za pomocą transformaty Fouriera kompleksu wykładniczego.
przyjrzymy się cosinusowi z częstotliwością F = A cykli / sekundę. Tę funkcję cosinusa można przepisać, dzięki Eulerowi, używając tożsamości:
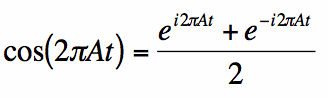 |
|---|
wraz z właściwością liniowości transformaty Fouriera można łatwo znaleźć transformatę Fouriera:
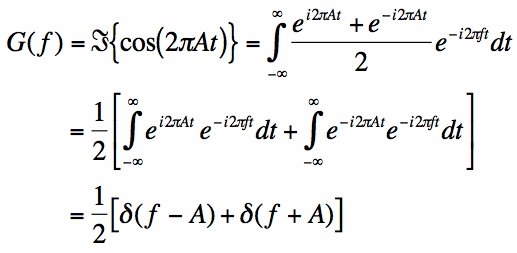 |
|---|
całki z ostatnich linii równania są łatwo oceniane na podstawie wyników z poprzedniej strony.Równanie stwierdza, że transformata Fouriera funkcji cosinusowej o częstotliwości a jest impulsem przy f = A i f = – A. Oznacza to, że cała energia sinusoidalnej funkcji o częstotliwości a jest w całości zlokalizowana na częstotliwościach podanych przez / f/ = A.
transformata Fouriera dla funkcji sinusowej może być wyznaczona równie szybko za pomocą tożsamości Eulera dla funkcji sinusoidalnej:
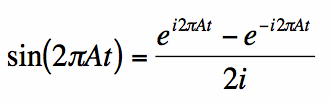 |
|---|
rezultatem jest:
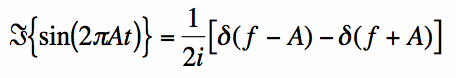 |
|---|
zauważ, że transformata Fouriera funkcji rzeczywistej, sin(t) ma urojoną transformatę Fouriera (brak części rzeczywistej). Jest to charakterystyczne dla funkcji nieparzystych.