Auf dieser Seite werden die Fourier-Transformationen für die Sinus-, Sinus- und Cosinusfunktion bestimmt. Das Ergebnis wird leicht unter Verwendung der Fourier-Transformation des komplexen Exponentials erhalten.
Wir betrachten den Kosinus mit der Frequenz f= A Zyklen / Sekunde. Diese Kosinusfunktion kann dank Euler unter Verwendung der Identität neu geschrieben werden:
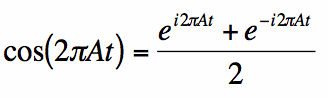 |
|---|
Zusammen mit der Linearitätseigenschaft der Fourier-Transformation kann die Fourier-Transformation leicht gefunden werden:
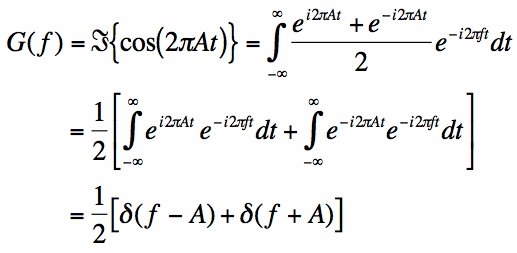 |
|---|
Die Integrale aus den letzten Zeilen der Gleichung können leicht anhand der Ergebnisse der vorherigen Seite ausgewertet werden.Gleichung besagt, dass die Fourier-Transformation der Kosinusfunktion der Frequenz A ein Impuls bei f = A und f=-A. Das heißt, die gesamte Energie einer Sinusfunktion der Frequenz A ist vollständig bei den durch /f/=A gegebenen Frequenzen lokalisiert.
Die Fourier-Transformation für die Sinusfunktion kann genauso schnell unter Verwendung der Eulerschen Identität für die Sinusfunktion bestimmt werden:
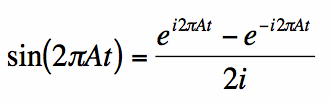 |
|---|
Das Ergebnis ist:
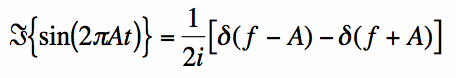 |
|---|
Beachten Sie, dass die Fourier-Transformation der reellen Funktion sin (t) eine imaginäre Fourier-Transformation hat (kein reeller Teil). Dies ist charakteristisch für ungerade Funktionen.