Sur cette page, les Transformées de Fourier pour la fonction sinus et cosinus sinus sont déterminées. Le résultat est facilement obtenu en utilisant la transformée de Fourier de l’exponentielle complexe.
Nous examinerons le cosinus avec la fréquence f = A cycles/seconde. Cette fonction cosinus peut être réécrite, grâce à Euler, en utilisant l’identité:
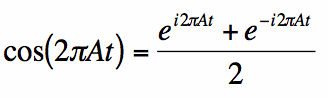 |
|---|
Avec la propriété de linéarité de la transformée de Fourier, la transformée de Fourier peut être facilement trouvée:
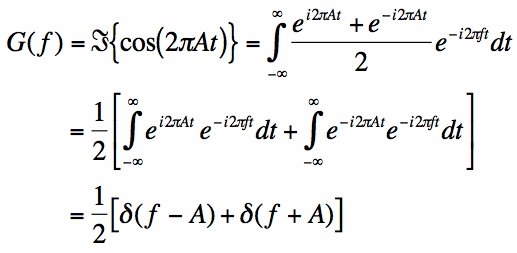 |
|---|
Les intégrales des dernières lignes de l’équation sont facilement évaluées à l’aide des résultats de la page précédente.L’équation indique que la transformée de fourier de la fonction cosinus de fréquence A est une impulsion à f = A et f =-A. C’est-à-dire que toute l’énergie d’une fonction sinusoïdale de fréquence A est entièrement localisée aux fréquences données par /f/=A.
La Transformée de Fourier pour la fonction sinusoïdale peut être déterminée tout aussi rapidement en utilisant l’identité d’Euler pour la fonction sinusoïdale:
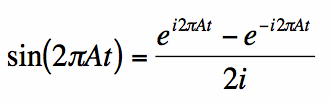 |
|---|
Le résultat est:
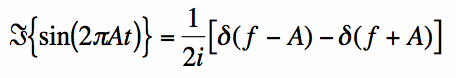 |
|---|
Notez que la Transformée de Fourier de la fonction réelle, sin(t) a une transformée de Fourier imaginaire (pas de partie réelle). Ceci est caractéristique des fonctions impaires.