期待値最大化の説明

期待最大化（EM）は、多様なアプリケーションで60年代と70年代に開発された古典的なアルゴリズ これは教師なしクラスタリングアルゴリズムとして使用でき、潜在的なディリクレ割り当て1、隠されたマルコフモデルのためのバウム–ウェルチアルゴリズム、医用画像化などのNLPアプリケーションに拡張されている。 最適化手順として、それは、多くの状況において、更新を解析的に計算することができるという主な利点を有する、勾配降下法などの代替法である。 それ以上に、最適化を考えるための柔軟なフレームワークです。

この記事では、簡単なクラスタリングの例から始めて、一般性のあるアルゴリズムについて説明します。

いくつかの測定値を持つさまざまなデータポイントがある状況を考えてみましょう。 それらを別のグループに割り当てたいと考えています。

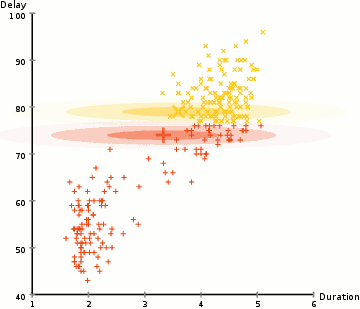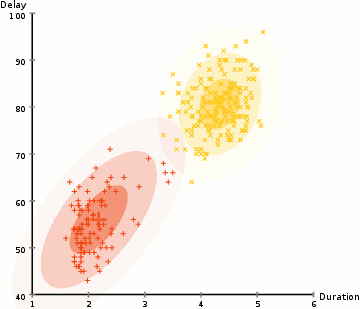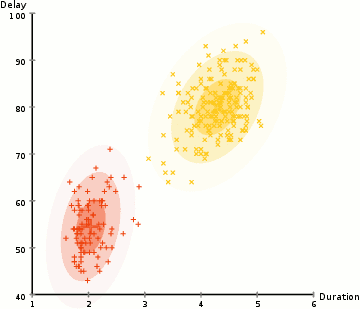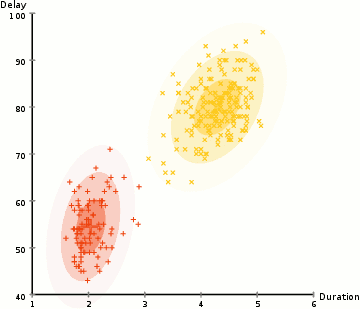
ここの例では、Yellowstoneの象徴的なOld Faithful間欠泉の噴火に関するデータがあります。 各噴火について、その長さと前回の噴火からの時間を測定しました。 噴火には2つの「タイプ」（図では赤と黄色）があり、噴火のタイプごとに結果のデータが（多変量）正規分布によって生成されると仮定することができます。 これは混合ガウスモデルと呼ばれています。

k-meansクラスタリングと同様に、これらの2つの分布/クラスターが何であるかをランダムに推測してから、2つのステップを交互に繰り返すことによ:

1. (期待値)各データポイントを確率的にクラスターに割り当てます。 この場合、赤のクラスターと黄色のクラスターから来た確率をそれぞれ計算します。
2. (最大化)クラスター内のポイント(最初のステップで割り当てられた確率で重み付け)に基づいて、各クラスターのパラメーター(加重平均位置と分散共分散行列)を更新します。

k-meansクラスタリングとは異なり、私たちのモデルは生成的であることに注意してください。 そして、モデルを再サンプルして、より多くの（偽の）データを生成することができます。

今、私たちは方程式を使って1次元の例をやろうとしています。

単一の測定値xを持つデータ点を考えます。これらは、それぞれが正規分布N(λ,λ2)に従う2つのクラスターによって生成されるとします。 最初のクラスターによって生成されるデータの確率はπです。

だから我々は5つのパラメータを持っています: 混合確率σ、および各クラスターの平均σおよび標準偏差σ。 私はそれらを総称してθと表記します。

としてまとめて表され、値xを持つデータポイントを観測する確率はいくらですか？ 正規分布の確率密度関数をσで表すとします。 記法を乱雑にしないようにするために、通常の分散の代わりに標準偏差をパラメータとして使用します。

を持つ点を観測する確率n点のデータセット全体を観測する確率（尤度）は次のようになります:

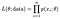
そして、私たちは通常、この対数を取って、私たちの積をより管理しやすい合計、対数尤度に変えることを選

私たちの目標はこれを最大化することです：観測したデータを観測する可能性が最も高いパラメータ（最尤推定量）にします。

さて、問題は、どのように最適化するのですか？ これを直接かつ分析的に行うことは、対数の合計のために難しいでしょう。

トリックは、我々がΔと呼ぶ潜在変数があると想像することです。 これは、ポイントがクラスター1またはクラスター2のどちらにあるかを決定するバイナリ(0/1値)変数です。 各点のΔがわかっていれば、パラメータの最尤推定値を計算するのは非常に簡単です。 便宜上、2番目のクラスターのΔが1であるという選択に一致するように、2番目のクラスター内にある点の確率にπを切り替えます。

合計が対数の外にあることに注意してください。 また、各Δを観測する可能性を説明するために余分な合計を拾います。

反事実的にΔを観測したと仮定すると、最尤推定値は簡単に形成されます。 Σについては、各クラスター内のサンプル平均を取り、σについては、同様に標準偏差（母集団式、これはMLEです）を取ります。 Λの場合、2番目のクラスター内の点のサンプル比率。 これらは、各パラメータの通常の最尤推定量です。

もちろん、Δは観測しませんでした。 これに対する解決策は、期待最大化アルゴリズムの中心です。 私たちの計画は:

1. パラメータの任意の最初の選択で始まります。
2. （期待値）はΔの推定値を形成する。
3. (最大化)最尤推定量を計算して、パラメータ推定値を更新します。
4. 収束するには、手順2と3を繰り返します。

繰り返しますが、同じことを行うk-meansクラスタリングについて考えると役立つかもしれません。 K-meansクラスタリングでは、各点を最も近い重心に割り当てます（期待ステップ）。 本質的には、これはΔの難しい推定値です。 それはクラスタの1つに1、他のすべてに0であるため、難しいです。 次に、重心をクラスタ内の点の平均に更新します（最大化ステップ）。 これはλの最尤推定量です。 K-meansクラスタリングでは、データの”モデル”には標準偏差がありません。 （「モデル」は生成的ではないため、恐怖の引用符で囲まれています）。

この例では、代わりにΔのソフト割り当てを行います。 私たちは時々これを責任と呼んでいます（各観測の各クラスターがどのように責任があるか）。 私たちは責任を①と表記します。

に対する各クラスターの責任μここで、この例の完全なアルゴリズムを書き留めることができます。 しかし、そうする前に、定義したシンボルの表をすばやく確認します（多くのものがありました）。

そしてここにアルゴリズムがあります:

クラスター1のσとσの推定値は類似していますが、代わりに1–σを重みとして使用していることに注意してく

アルゴリズムの例を挙げたので、あなたはうまくいけばそれの感触を持っています。 アルゴリズムの一般的な説明に移ります。 これは基本的に、少し複雑な変数で行ったすべてのことをドレスアップすることになります。 そして、それはなぜそれが機能するのかを説明する立場に私たちを置くでしょう。

一般的な期待最大化

一般的な設定に移りましょう。 ここに設定があります:

1. 私たちはどんな形のデータXを持っています。
2. 我々はまた、観測されていない（潜在的な）データΔもあると仮定します。
3. パラメータλを持つモデルがあります。
4. 対数尤度λ(λ;X,Δ)を計算する能力があります。 具体的には、私たちのデータを観察する確率のログと、パラメータを与えられた潜在変数の指定された割り当て。
5. また、パラメータのセットが与えられた条件付き分布Δ|Xを計算するためにモデルを使用することもできます。 これをP(Δ|X;θ)とする。
6. その結果、対数尤度λ(λ;X)を計算することができます。 これは、パラメータが与えられたデータを観察する確率のログです（潜在変数の割り当てを想定せずに）。

確率を表すためにPを使用して、我々は今、書くためにチェーンルールを使用することができます:

表記はここで微妙なことがあります。 すべての3つの項は、パラメータλを与えられたものとして取ります。

1. 左の最初の項は、データを観測する確率と指定された潜在変数割り当てです。
2. 右側の最初の項は、観測されたデータが与えられた潜在変数の指定された割り当ての確率です。
3. 最後の項はデータを観測する確率です。

対数を取って項を並べ替えることができます。 次に、2行目で表記法の変更を行います（そしてそれを混乱させます。 私を責めないで、私はそれを発明しなかった):

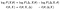
最初の二つの用語については、それは私たちの前の例の文脈でそれらが何であるかを見直す価値があります。 最初のσ（σ;X）は、最適化したいものです。 ２つ目のσ（σ；Ｘ，Δ）は解析的に扱いやすいものであった。

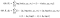
さて、パラメータεを与えられた条件付き分布Δ|Xを計算できると言ったことを覚えておいてください。 これは物事が野生になる場所です。

私たちは、同じパラメータの第二のセットを導入しようとしている、それを呼び出すθʹ。 私はまた、この”ê”が持っているもののように、それの上に帽子（サーカムフレックス）でそれを示すこともあります。2このパラメータのセットを現在の推定値と考えてください。 現在の数式のθは、推定値を改善するために最適化されます。

ここで、条件付き分布Δ|X、σに関する対数尤度の期待値、すなわちデータと現在のパラメータ推定値を与えられた潜在変数の分布を取ります。

左側の用語は、Δを知っていない/気にしないので変更されません（定数です）。 ここでも、期待値はΔの可能な値を超えています。 あなたが私たちの例に関して従っているならば、Δがεに置き換えられるように期待値を取った後、用語ε（ε;X、Δ）は変化します。

さて、非常に迅速に、私たちがここで起こっている表記の悪夢を改善するために、私たちが右側に持っている二つの期待のための速記表記法を紹介し

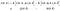
アルゴリズムは次のようになります:

なぜそれが働くのか

これがうまくいくことを証明するための重い持ち上げは、関数R(λ,λ)を考慮するこ この主張は、ε=εのときRが最大化されるというものである。 完全な証明の代わりに、Rが計算するものについて考えてみましょう。 データXへの依存性（期待値を取っている分布と尤度関数との間で共有されている）を取り除くと、Rはschematically的になります

の概略形式言い換えれば、我々は二つの確率分布を持っています。 一方（μでパラメータ化された）を使用してデータδを生成し、もう一方（μでパラメータ化された）を使用して見たものの確率を計算します。 Δがちょうど単一の数を表し、分布が確率密度関数を持っている場合、我々は書くことができます（再び、模式的に)

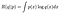
私は、2つの確率分布間の距離の（ほぼ）尺度であるKullback-Leibler（KL）発散のそれに似た形でこれを示唆的に書いています。 定数R(p||p)からr(q||p)を減算すると、0で下に制限され、q=pのときは0にのみなるKL発散が得られます（分布pからの距離3 0はp自体です）。 これはKL-発散に関する標準的な結果であり、Jensenの不等式で証明することができます。⁴

今、残っている唯一のことは、私たちの更新ステップの前後の尤度の違いを考慮することです:

私たちはQを最大化するために新しいパラメータを選択したので、最初の項は間違いなく正です。 上記の引数では、rは古いパラメータを最初の引数として取ることによって最大化されるため、2番目の項は負でなければなりません。 正のマイナス負は正です。 したがって、各更新ステップで可能性が増加しています。 各ステップは、物事をより良くすることが保証されています。

また、Qを最適化する必要がないことに注意してください。 私たちがしなければならないのは、それをより良くするためのいくつかの方法を見つけることであり、私たちの更新はまだ

結論

うまくいけば、あなたは今、アルゴリズムのための良い感触を持っています。 数学の面では、重要な方程式は以下の尤度にすぎません。 その後、古いパラメータ（期待ステップ）に関して期待を取り、右側の最初の項を最適化するだけで問題ないことを示します。 混合ガウスモデルの例で動機づけられているように、この第二項はしばしば最適化が容易です。 私たちが心配する必要はありません第三の用語は、それが台無しに何もしません。

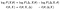
少し戻って、私はEMアルゴリズムのパワーと有用性を強調したいと思います。 まず、潜在変数を導入し、潜在変数を交互に扱う（パラメータを固定および既知とする）ことと、パラメータを扱う（潜在変数を固定および既知とする）ことによ これは、さまざまな状況で表示されます強力なアイデアです。

第二に、アルゴリズムは勾配の計算に依存しないため、本質的に高速です。 モデルを解析的に解くことができるときはいつでも（線形回帰を使用するように）、それはより速くなるでしょう。 そして、これは私たちが解析的に難治性の問題を取り、それらの一部を解析的に解くことができ、その力を反復的な文脈に拡張することができます。

最後に、EMアルゴリズムについてもっと言うことがたくさんあることに注意したいと思います。 これは、最大化ステップを行う他の形式と変分ベイズ法に一般化し、さまざまな方法で理解することができます（例えば、最大化-最大化または統計多様体（e-接続とm-接続）上の相互双対アフィン接続の下での部分多様体への交互投影として）。 将来的にはそれについての詳細！