Explication de la maximisation des attentes

La maximisation des attentes (EM) est un algorithme classique développé dans les années 60 et 70 avec diverses applications. Il peut être utilisé comme algorithme de clustering non supervisé et s’étend aux applications de PNL telles que l’allocation de Dirichlet latente 1, l’algorithme de Baum-Welch pour les modèles de Markov cachés et l’imagerie médicale. En tant que procédure d’optimisation, c’est une alternative à la descente de gradient et autres avec l’avantage majeur que, dans de nombreuses circonstances, les mises à jour peuvent être calculées de manière analytique. Plus que cela, c’est un cadre flexible pour réfléchir à l’optimisation.

Dans cet article, nous allons commencer par un exemple de clustering simple, puis discuter de l’algorithme en général.

Considérez la situation où vous avez une variété de points de données avec certaines mesures d’entre eux. Nous souhaitons les affecter à différents groupes.

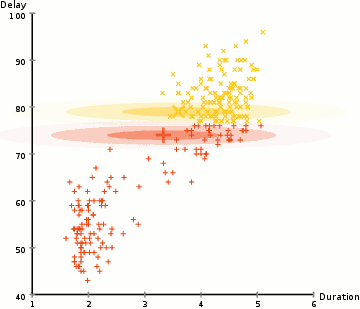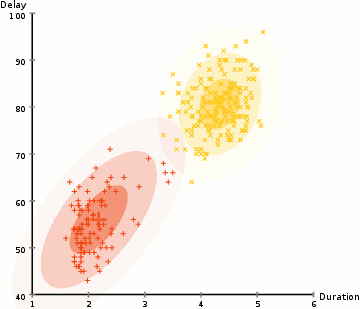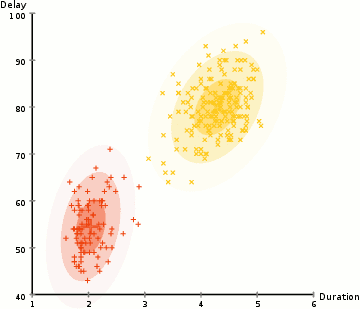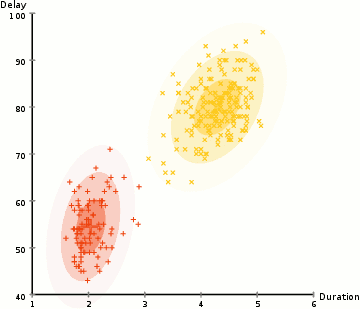
Dans l’exemple ici, nous avons des données sur les éruptions de l’emblématique geyser Old Faithful à Yellowstone. Pour chaque éruption, nous avons mesuré sa durée et le temps écoulé depuis l’éruption précédente. Nous pourrions supposer qu’il existe deux « types » d’éruptions (rouge et jaune dans le diagramme), et pour chaque type d’éruption, les données résultantes sont générées par une distribution normale (multivariée). C’est ce qu’on appelle un modèle de mélange Gaussien, incidemment.

Similaire au clustering k-means, nous commençons par une supposition aléatoire de ce que sont ces deux distributions / clusters, puis nous procédons à une amélioration itérative en alternant deux étapes:

1. ( Attente) Attribuent chaque point de données à un cluster de manière probabiliste. Dans ce cas, nous calculons la probabilité qu’il provienne respectivement du cluster rouge et du cluster jaune.
2. (Maximisation) Mettre à jour les paramètres de chaque cluster (emplacement moyen pondéré et matrice variance-covariance) en fonction des points du cluster (pondérés par leur probabilité attribuée dans la première étape).

Notez que contrairement au clustering k-means, notre modèle est génératif: il prétend nous indiquer le processus par lequel les données ont été générées. Et nous pourrions, à notre tour, rééchantillonner le modèle pour générer plus de (fausses) données.

Vous l’avez? Maintenant, nous allons faire un exemple à 1 dimension avec des équations.

Considérons les points de données avec une seule mesure x. Nous supposons qu’ils sont générés par 2 clusters suivant chacun une distribution normale N (μ, σ2). La probabilité que des données soient générées par la première grappe est π.

Nous avons donc 5 paramètres: une probabilité de mélange π, et une moyenne μ et un écart type σ pour chaque grappe. Je les désignerai collectivement par θ.

Quelle est la probabilité d’observer un point de données de valeur x ? Soit la fonction de densité de probabilité de la distribution normale désignée par ϕ. Pour garder la notation moins encombrée, j’utiliserai l’écart-type comme paramètre au lieu de la variance habituelle.

La probabilité (probabilité) d’observer l’ensemble de nos données de n points est:

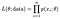
Et nous choisissons généralement de prendre le logarithme de ceci pour transformer notre produit en une somme plus gérable, la log-vraisemblance.

Notre objectif est de maximiser ceci: nous voulons que nos paramètres soient ceux où il est le plus probable que nous observions les données que nous avons observées (un Estimateur de maximum de Vraisemblance).

Maintenant, la question est: comment allons-nous l’optimiser? Le faire directement et analytiquement serait délicat à cause de la somme dans le logarithme.

L’astuce consiste à imaginer qu’il existe une variable latente que nous appellerons Δ. C’est une variable binaire (à valeur 0/1) qui détermine si un point se trouve dans le cluster 1 ou le cluster 2. Si nous connaissons Δ pour chaque point, il serait très facile de calculer les estimations de maximum de vraisemblance de nos paramètres. Pour plus de commodité pour faire correspondre notre choix de Δ étant 1 pour le deuxième groupe, nous changerons π pour être la probabilité qu’un point se trouve dans le deuxième groupe.

Notez que les sommes sont maintenant en dehors du logarithme. De plus, nous prenons une somme supplémentaire pour tenir compte de la probabilité d’observer chaque Δ.

En supposant par contre que nous avons observé Δ, les estimations du maximum de vraisemblance sont faciles à former. Pour μ, prenez la moyenne de l’échantillon dans chaque grappe; pour σ, de même l’écart-type (la formule de la population, qui est la MLE). Pour π, la proportion d’échantillon de points dans le deuxième groupe. Ce sont les estimateurs habituels du maximum de vraisemblance pour chaque paramètre.

Bien sûr, nous n’avons pas observé Δ. La solution à cela est au cœur de l’algorithme de maximisation des attentes. Notre plan est:

1. Commencez par un choix initial arbitraire de paramètres.
2. (Espérance) Forment une estimation de Δ.
3. (Maximisation) Calculez les estimateurs de maximum de vraisemblance pour mettre à jour notre estimation de paramètre.
4. Répétez les étapes 2 et 3 jusqu’à la convergence.

Encore une fois, vous trouverez peut-être utile de penser au clustering k-means, où nous faisons la même chose. Dans le clustering k-means, nous attribuons chaque point au centroïde le plus proche (pas d’attente). En substance, il s’agit d’une estimation difficile de Δ. Difficile car c’est 1 pour l’un des clusters et 0 pour tous les autres. Ensuite, nous mettons à jour les centroïdes pour être la moyenne des points du cluster (étape de maximisation). C’est l’estimateur de maximum de vraisemblance pour μ. Dans le clustering k-means, le « modèle » des données n’a pas d’écart-type. (Le « modèle » est entre guillemets car il n’est pas génératif).

Dans notre exemple, nous ferons plutôt une affectation douce de Δ. Nous appelons parfois cela la responsabilité (quelle est la responsabilité de chaque cluster pour chaque observation). Nous désignerons la responsabilité comme ɣ.

Maintenant, nous pouvons écrire l’algorithme complet pour cet exemple. Mais avant de le faire, nous allons rapidement passer en revue un tableau de symboles que nous avons définis (il y en avait beaucoup).

Et voici l’algorithme:

Note que les estimations de μ et σ pour le cluster 1 sont analogues mais en utilisant 1-ɣ comme poids à la place.

Maintenant que nous avons donné un exemple de l’algorithme, vous en avez, espérons-le, une idée. Nous allons passer à la discussion de l’algorithme en général. Cela revient essentiellement à habiller tout ce que nous avons fait avec des variables légèrement plus compliquées. Et cela nous mettra en mesure d’expliquer pourquoi cela fonctionne.

Maximisation des attentes en général

Passons au paramètre général. Voici la configuration:

1. Nous avons des données X de quelque forme que ce soit.
2. Nous posons qu’il existe également des données non observées (latentes) Δ, encore une fois de quelque forme que ce soit.
3. Nous avons un modèle avec les paramètres θ.
4. Nous avons la capacité de calculer la log-vraisemblance ℓ(θ; X, Δ). Plus précisément, le journal de la probabilité d’observer nos données et les affectations spécifiées des variables latentes compte tenu des paramètres.
5. Nous avons également la possibilité d’utiliser le modèle pour calculer la distribution conditionnelle Δ|X à partir d’un ensemble de paramètres. On notera ce P (Δ/X ; θ).
6. Par conséquent, nous pouvons calculer la log-vraisemblance ℓ(θ; X). C’est le journal de la probabilité d’observer nos données compte tenu des paramètres (sans assumer d’affectation pour les variables latentes).

En utilisant P pour désigner la probabilité, nous pouvons maintenant utiliser la règle de chaîne pour écrire:

La notation peut être subtile ici. Les trois termes prennent les paramètres θ comme étant donnés.

1. Le premier terme à gauche est la probabilité d’observer les données et une affectation de variable latente spécifiée.
2. Le premier terme à droite est la probabilité de l’affectation spécifiée des variables latentes compte tenu des données observées.
3. Le dernier terme est la probabilité d’observer les données.

Nous pouvons prendre des logarithmes et réorganiser les termes. Ensuite, à la deuxième ligne, nous ferons un changement de notation (et confus à ce sujet. Ne me blâme pas, je ne l’ai pas inventé):

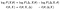
Pour les deux premiers termes, il vaut la peine de revoir ce qu’ils sont dans le contexte de notre exemple précédent. Le premier,θ(θ; X), est celui que nous voulons optimiser. Le second,θ(θ; X, Δ), était celui qui était analytiquement traçable.

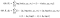
Maintenant, rappelez-vous que j’ai dit que nous pouvons calculer la distribution conditionnelle Δ | X compte tenu des paramètres θ? C’est là que les choses deviennent folles.

Nous allons introduire un deuxième ensemble des mêmes paramètres, appelez-le θʹ. Je le désignerai aussi parfois avec un chapeau (circonflexe) dessus, comme celui que possède ce « ê ».2 Considérez cet ensemble de paramètres comme notre estimation actuelle. Le θ actuellement dans nos formules sera optimisé pour améliorer notre estimation.

Maintenant, nous allons prendre l’attente des probabilités log par rapport à la distribution conditionnelle Δ | X, θʹ – à savoir la distribution de nos variables latentes compte tenu des données et de notre estimation des paramètres actuels.

Le terme sur le côté gauche ne change pas car il ne sait pas / se soucie de Δ de toute façon (c’est une constante). Encore une fois, l’attente est supérieure aux valeurs possibles de Δ. Si vous suivez notre exemple, le terme ℓ(θ; X, Δ) change après que nous ayons pris l’attente pour que Δ soit remplacé par ɣ.

Maintenant, très rapidement, pour améliorer le cauchemar notationnel que nous avons ici, introduisons la notation sténographique pour les deux attentes que nous avons du côté droit

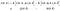
L’algorithme devient:

Pourquoi cela fonctionne

Le travail lourd pour prouver que cela fonctionnera est de considérer la fonction R (θ, θʹ). L’affirmation est que R est maximisé lorsque θ = θʹ. Au lieu d’une preuve complète, réfléchissons à ce que R calcule. En éliminant la dépendance à l’égard des données X (qui est partagée entre la distribution sur laquelle nous prenons une attente et la fonction de vraisemblance), R devient schématiquement

En d’autres termes, nous avons deux distributions de probabilité. Nous utilisons l’un (paramétré par θʹ) pour générer des données Δ et nous utilisons l’autre (paramétré par θ) pour calculer la probabilité de ce que nous avons vu. Si Δ ne représente qu’un seul nombre et que les distributions ont des fonctions de densité de probabilité, on pourrait écrire (encore une fois, schématiquement)

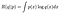
J’ai suggéré ceci sous une forme similaire à celle de la divergence de Kullback-Leibler (KL) qui est (presque) une mesure de la distance entre deux distributions de probabilité. Si nous soustrayons R(q // p) d’une constante R(p||p), nous obtiendrons la KL-divergence qui est bornée en dessous de 0 et n’est que 0 lorsque q = p. (La seule chose à une distance30 de la distribution p est p elle-même). En d’autres termes, R est maximisé lorsque q = p. C’est un résultat standard sur la divergence KL et peut être prouvé avec l’inégalité de Jensen.⁴

Maintenant, la seule chose à faire est de considérer la différence entre les probabilités avant et après notre étape de mise à jour:

Nous avons choisi les nouveaux paramètres pour maximiser Q, donc le premier terme est définitivement positif. Par l’argument ci-dessus, R est maximisé en prenant les anciens paramètres comme premier argument, de sorte que le deuxième terme doit être négatif. Positif moins négatif est positif. Par conséquent, la probabilité a augmenté à chaque étape de mise à jour. Chaque étape est garantie pour améliorer les choses.

Notez également que nous n’avons pas à optimiser Q. Tout ce que nous devons, c’est trouver un moyen de l’améliorer et nos mises à jour sont toujours garanties pour améliorer les choses.

Conclusion

J’espère que vous avez maintenant une bonne idée de l’algorithme. En termes de mathématiques, l’équation clé est juste les probabilités ci-dessous. Après cela, nous prenons simplement les attentes par rapport aux anciens paramètres (l’étape d’attente) et montrons que nous sommes bien d’optimiser simplement le premier terme du côté droit. Comme nous l’avons motivé avec l’exemple du modèle de mélange Gaussien, ce deuxième terme est souvent plus facile à optimiser. Le troisième mandat dont nous n’avons pas à nous inquiéter, ça ne gâchera rien.

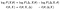
En prenant un peu de recul, je veux souligner la puissance et l’utilité de l’algorithme EM. Tout d’abord, cela représente l’idée que nous pouvons introduire des variables latentes puis calculer en traitant alternativement les variables latentes (en prenant les paramètres comme fixes et connus) et en traitant les paramètres (en prenant les variables latentes comme fixes et connues). C’est une idée puissante que vous verrez dans une variété de contextes.

Deuxièmement, l’algorithme est intrinsèquement rapide car il ne dépend pas du calcul des gradients. Chaque fois que vous pouvez résoudre un modèle analytiquement (comme en utilisant une régression linéaire), ce sera plus rapide. Et cela nous permet de prendre des problèmes analytiquement insolubles et d’en résoudre certaines parties de manière analytique, en étendant ce pouvoir à un contexte itératif.

Enfin, je tiens à noter qu’il y a beaucoup plus à dire sur l’algorithme EM. Il se généralise à d’autres formes de réalisation de l’étape de maximisation et aux techniques bayésiennes variationnelles et peut être compris de différentes manières (par exemple comme maximisation-maximisation ou comme projections alternées à un sous-nombre sous des connexions affines mutuellement duales sur une variété statistique (les connexions e et m)). Plus à ce sujet à l’avenir!