odotuksen maksimointi selitetty

odotuksen maksimointiin (em) on 60-ja 70-luvuilla kehitetty klassinen algoritmi, jolla on erilaisia sovelluksia. Sitä voidaan käyttää valvomattomana ryhmittelyalgoritmina ja se ulottuu NLP-sovelluksiin, kuten piilevään Dirichlet ’ n Allocation1: een, Baum–Welchin algoritmiin piilotetuille Markov-malleille ja lääketieteelliseen kuvantamiseen. Optimointimenettelynä se on vaihtoehto gradienttilaskeutumiselle ja vastaaville, sillä suuri etu on, että monissa olosuhteissa päivitykset voidaan laskea analyyttisesti. Lisäksi se on joustava kehys optimoinnin ajattelulle.

tässä artikkelissa aloitetaan yksinkertaisella ryhmittelyesimerkillä ja keskustellaan sitten algoritmista yleisellä tasolla.

tarkastellaan tilannetta, jossa on erilaisia datapisteitä, joista on joitakin mittauksia. Haluamme jakaa heidät eri ryhmiin.

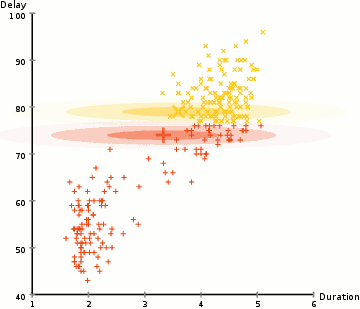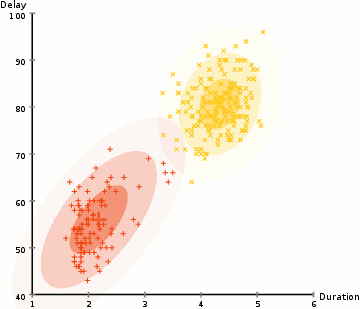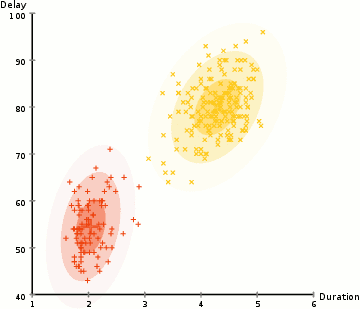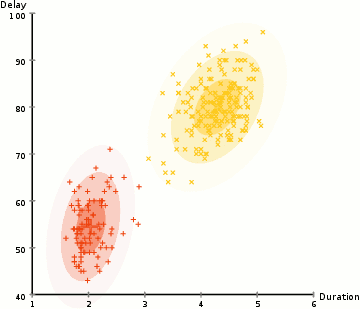
tässä esimerkissä on tietoja ikonisen vanhan uskollisen geysirin purkauksista Yellowstonessa. Jokaiselle purkaukselle on mitattu sen pituus ja aika edellisen purkauksen jälkeen. Voisimme olettaa, että purkauksia on kaksi ”tyyppiä” (punainen ja keltainen kuvassa), ja kullekin purkaustyypille tuloksena oleva tieto syntyy (monimuuttujalla) normaalijakaumalla. Tätä kutsutaan muuten Gaussin Sekoitusmalliksi.

kuten k-tarkoittaa ryhmittelyä, aloitetaan satunnaisella arvauksella, mitä nämä kaksi jakaumaa/klusteria ovat, ja edetään sitten iteratiivisesti parempaan vuorotellen kahdella askeleella:

1. (odotus) Määritä jokainen datapiste klusterille todennäköisyydellä. Tässä tapauksessa laskemme Todennäköisyys se tuli punainen klusterin ja keltainen klusterin vastaavasti.
2. (maksimointi) Päivitä kunkin klusterin parametrit (painotettu keskikohta ja varianssi-kovarianssimatriisi) klusterin pisteiden perusteella (painotettuna niiden ensimmäisessä vaiheessa annetulla todennäköisyydellä).

huomaa, että toisin kuin k-tarkoittaa ryhmittelyä, mallimme on generatiivinen: sen väitetään kertovan prosessin, jolla tieto on luotu. Ja voisimme vuorostamme uudelleen näytteen malli tuottaa enemmän (väärennettyä) dataa.

Saitko sen? Nyt aiomme tehdä 1-ulotteinen esimerkki yhtälöt.

tarkastellaan datapisteitä yhdellä mittauksella x. oletamme, että nämä syntyvät 2 klusterista, joista kukin seuraa normaalijakaumaa N(μ, σ2). Ensimmäisen klusterin tuottaman tiedon todennäköisyys on π.

joten meillä on 5 parametria: sekoitustodennäköisyys π ja keskiarvo μ ja keskihajonta σ kullekin klusterille. Merkitsen ne kollektiivisesti θ: na.

mikä on todennäköisyys havainnoida datapoint arvolla x? Olkoon normaalijakauman todennäköisyys-tiheysfunktio merkittynä ϕ. Jotta notaatio pysyisi vähemmän sekavana, käytän parametrina standardipoikkeamaa tavanomaisen varianssin sijaan.

koko n-pisteen havaintoaineistomme todennäköisyys (todennäköisyys) on:

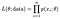
ja tyypillisesti valitsemme tämän logaritmin muuttaaksemme tuotteemme helpommin hallittavaksi summaksi, log-todennäköisyydeksi.

tavoitteenamme on maksimoida tämä: haluamme parametriemme olevan ne, joissa on todennäköisintä, että havaitsemme havaitsemamme tiedot (Maksimitodennäköisyyden estimaattori).

nyt kysymys kuuluu, miten optimoimme sen? Sen tekeminen suoraan ja analyyttisesti olisi hankalaa logaritmin summan vuoksi.

temppu on kuvitella, että on olemassa piilevä muuttuja, jota kutsumme Δ: ksi. Se on binäärinen (0/1-arvoinen) muuttuja, joka määrittää, onko piste klusterissa 1 vai klusterissa 2. Jos tietäisimme Δ: N jokaiselle pisteelle, olisi erittäin helppoa laskea parametriemme maksimitodennäköisyysarviot. Mukavuuden vastaamaan meidän valinta Δ on 1 toisen klusterin, vaihdamme π on todennäköisyys kohta on toisen klusterin.

huomaa, että summat ovat nyt logaritmin ulkopuolella. Lisäksi poimimme ylimääräisen summan, joka selittää todennäköisyyden tarkkailla jokaista Δ: tä.

jos oletetaan vastatodennäköisesti, että havaitsimme Δ: n, suurimmat todennäköisyysarviot on helppo muodostaa. Μ: lle otetaan näytteen keskiarvo kussakin ryppäässä; σ: lle samoin keskihajonta (populaatiokaava, joka on MLE). Π: n osalta toisen klusterin pisteiden otossuhde. Nämä ovat tavanomaiset maksimitodennäköisyyden estimaattorit kullekin parametrille.

ei tietenkään havaittu Δ. Ratkaisu tähän on odotuksen maksimointialgoritmin sydän. Suunnitelmamme on:

1. Aloita mielivaltaisella parametrivalinnalla.
2. (odotus) muodostaa estimaatin Δ.
3. (maksimointi) laske maksimitodennäköisyysestimaattorit parametriarviomme päivittämiseksi.
4. Toista vaiheet 2 ja 3 konvergenssiin.

taas voi olla hyödyllistä miettiä k-tarkoittaa ryhmittelyä, jossa toimitaan samalla tavalla. K-tarkoittaa ryhmittelyä, annamme jokaisen pisteen lähimmälle centroidille (odotusvaihe). Pohjimmiltaan kyseessä on kova arvio Δ-arvosta. Vaikea, koska se on 1 yksi klustereita ja 0 kaikille muille. Sitten päivitämme centroids olla keskiarvo pistettä klusterin (maksimointi vaihe). Tämä on maksimitodennäköisyyden estimaattori μ: lle. K-tarkoittaa ryhmittelyä, jossa datan ”mallilla” ei ole keskihajontaa. (”Malli” on pelottavissa lainauksissa, koska se ei ole generatiivinen).

esimerkissämme teemme sen sijaan pehmeän tehtävän Δ. Joskus kutsumme tätä vastuuksi (kuinka vastuussa kukin klusteri on jokaisesta havainnosta). Me ilmaisemme vastuun as ɣ.

nyt voimme kirjoittaa tähän esimerkkiin koko algoritmin. Mutta ennen kuin teemme niin, käymme nopeasti läpi taulukon symboleista, jotka olemme määritelleet (niitä oli paljon).

ja tässä on algoritmi:

huomaa, että klusterin 1 estimaatit μ Ja σ ovat analogisia, mutta käyttävät sen sijaan painoina 1–ɣ.

nyt kun olemme antaneet esimerkin algoritmista, sinulla on toivottavasti tuntuma siihen. Siirrymme keskustelemaan algoritmista yleisesti. Tämä tarkoittaa käytännössä sitä, että verhoamme kaiken tekemämme hieman monimutkaisemmilla muuttujilla. Se antaa meille mahdollisuuden selittää, miksi se toimii.

odotuksen maksimointi yleisesti

siirrytään yleisasetukseen. Tässä on asetukset:

1. meillä on tietoja X missä muodossa tahansa.
2. on myös havaitsematonta (piilevää) tietoa Δ, jälleen missä muodossa tahansa.
3. meillä on malli, jossa on parametrit θ.
4. meillä on kyky laskea log-todennäköisyys ℓ (θ; X, Δ). Erityisesti loki todennäköisyys havainnoida meidän Tiedot ja määritellyt tehtävät latentti muuttujia annetaan parametrit.
5. mallin avulla voidaan laskea myös ehdollinen jakauma Δ|X, joka on annettu parametreille. Merkitään tämä P (Δ / X; θ).
6. näin ollen voidaan laskea log-todennäköisyys ℓ(θ; X). Tämä on loki todennäköisyys havainnoida meidän tiedot annetaan parametrit (olettamatta tehtävän latentti muuttujia).

käyttämällä P: tä ilmaisemaan todennäköisyyttä, voidaan nyt kirjoittaa ketjusääntöä:

notaatio voi olla tässä hienovarainen. Kaikki kolme termiä ottavat parametrit θ annettuna.

1. ensimmäinen termi vasemmalla on datan havainnoinnin todennäköisyys ja määritelty latentin muuttujan määritys.
2. ensimmäinen oikeanpuoleinen termi on havaitun aineiston perusteella latenttien muuttujien määritetyn jaon todennäköisyys.
3. viimeinen termi on tiedon havainnoinnin todennäköisyys.

voimme ottaa logaritmeja ja järjestellä termejä uudelleen. Sitten toisella rivillä teemme notaatio muutos (ja sekava yksi, että. Älä minua syytä, en keksinyt sitä.):

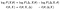
kahden ensimmäisen termin osalta on syytä tarkastella, mitä ne ovat edellisen esimerkkimme yhteydessä. Ensimmäinen, ℓ (θ; X), on se, jonka haluamme optimoida. Toinen, ℓ(θ; X, Δ), oli analyyttisesti jäljitettävissä oleva.

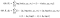
nyt, Muistatko, että sanoin, että voimme laskea ehdollisen jakauman Δ / X parametrien θ perusteella? Täällä tilanne menee villiksi.

otamme käyttöön saman parametrin toisen joukon, nimeltään θʹ. Aion myös joskus kuvaamaan sitä hattu (circumflex) sen yli, kuten yksi tämä ”ê” on.2 ajattele tätä parametrijoukkoa nykyisenä arvionamme. Kaavoissamme tällä hetkellä oleva θ optimoidaan arviomme parantamiseksi.

nyt otamme lokin likiarvon odotuksen ehdollisen jakauman Δ / X, θʹ suhteen-nimittäin latenttien muuttujiemme jakauman datan ja nykyisen parametrin estimaatin suhteen.

termi vasemmalla puolella ei muutu, koska se ei tiedä/välitä Δ anyways (se on vakio). Jälleen odotus on yli mahdollisten arvojen Δ. Jos seuraat yhdessä suhteessa esimerkkiimme, termi ℓ (θ; X, Δ) muuttuu sen jälkeen, kun otamme odotuksen niin, että Δ korvataan ɣ: lla.

now, very quickly, to ameliorate the notational nightmare we ’ve got going on here, let’ s introduct shorthand notation for the two expectations we have on the right side side

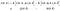
algoritmista tulee:

miksi se toimii

raskas nosto tämän toimivuuden todistamiseksi on funktion r(θ, θʹ) tarkasteleminen. Väitteen mukaan R maksimoidaan, kun θ=θʹ. Sen sijaan, että täysi todiste let ’ s ajatella, mitä R laskee. Stripping pois riippuvuus data X (joka on jaettu jakauma otamme odotus yli ja todennäköisyys funktio), R kaavamaisesti tulee

toisin sanoen meillä on kaksi todennäköisyysjakaumaa. Käytämme yhtä (parametrisoitu θʹ) datan tuottamiseen Δ ja toista (parametrisoitu θ) laskemaan näkemämme todennäköisyyden. Jos Δ edustaa vain yhtä lukua ja jakaumilla on todennäköisyystiheysfunktiot, voisimme kirjoittaa (jälleen, kaavamaisesti)

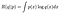
olen suggestiivisesti kirjoittanut tämän samanlaiseen muotoon kuin Kullback-Leibler (KL) Divergenssi, joka on (lähes) kahden todennäköisyysjakauman välisen etäisyyden mitta. Jos vähennämme r: n(q||p) vakiosta R (p||p), saamme KL-divergenssin, joka rajoittuu alle arvoon 0 ja on vain 0, kun q=p. (ainoa asia, jonka distanssi3 0 jakaumasta p on p itse). Toisin sanoen, R on maksimoitu, kun q=p. Tämä on vakiotulos noin KL-divergenssi ja voidaan todistaa Jensenin epäyhtälö.⁴

nyt on enää mietittävä, mitä eroa on likelikaatioilla ennen ja jälkeen päivitysvaiheen:

jälkeen valitsimme uudet parametrit Q: n maksimoimiseksi, joten ensimmäinen termi on ehdottomasti positiivinen. Edellä esitetyllä argumentilla R maksimoidaan ottamalla Vanhat parametrit ensimmäiseksi argumentikseen, joten toisen termin on oltava negatiivinen. Positiivinen miinus negatiivinen on positiivinen. Siksi todennäköisyys on kasvanut jokaisessa päivitysvaiheessa. Jokainen askel parantaa varmasti asioita.

Huomaa myös, että meidän ei tarvitse optimoida Q: ta. Meidän täytyy vain löytää jokin tapa tehdä siitä parempi ja päivityksemme ovat edelleen taatusti tehdä asiat paremmin.

johtopäätös

toivottavasti nyt on hyvä tuntuma algoritmiin. Matematiikan kannalta keskeinen yhtälö on vain likelikaatiot alla. Sen jälkeen, me vain ottaa odotuksia suhteessa vanhoihin parametreihin (odotusvaihe) ja osoittaa, että olemme kunnossa vain optimoida ensimmäisen kauden oikealla puolella. Koska olemme motivoituneita Gaussin seos malli esimerkki, tämä toinen termi on usein helpompi optimoida. Kolmas kausi, josta ei tarvitse huolehtia, ei sotke mitään.

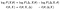
astun hieman taaksepäin ja haluan korostaa EM-algoritmin tehoa ja hyödyllisyyttä. Ensinnäkin se edustaa ajatusta, että voimme ottaa käyttöön piileviä muuttujia ja sitten laskea käsittelemällä vuorotellen latentteja muuttujia (ottamalla parametrit kiinteiksi ja tunnetuiksi) ja käsittelemällä parametreja (ottamalla latentit muuttujat kiinteiksi ja tunnetuiksi). Tämä on voimakas ajatus, että näet eri yhteyksissä.

toiseksi algoritmi on luonnostaan nopea, koska se ei riipu laskentagradienteistä. Aina kun voit ratkaista mallin analyyttisesti (kuten käyttämällä lineaarista regressiota), se tulee olemaan nopeampi. Ja tämä antaa meille mahdollisuuden ottaa analyyttisesti hankalia ongelmia ja ratkaista osia niistä analyyttisesti, ulottamalla että valta iteratiivinen yhteydessä.

lopuksi haluan todeta, että EM-algoritmista on paljon muutakin sanottavaa. Se yleistää muihin maksimointivaiheen tekemisen muotoihin ja variationaalisiin Bayesilaisiin tekniikoihin, ja se voidaan ymmärtää eri tavoin (esimerkiksi maksimointi-maksimointi tai alternoiva projektio submanifoldille tilastollisella monistolla (E – ja m – liitännät)). Lisää siitä tulevaisuudessa!