Ein vielseitiger Algorithmus für Clustering, NLP und mehr
Expectation Maximization (EM) ist ein klassischer Algorithmus, der in den 60er und 70er Jahren mit vielfältigen Anwendungen entwickelt wurde. Es kann als unüberwachter Clustering-Algorithmus verwendet werden und erstreckt sich auf NLP–Anwendungen wie latente Dirichlet-Zuordnung1, den Baum-Welch-Algorithmus für Hidden-Markov-Modelle und die medizinische Bildgebung. Als Optimierungsverfahren ist es eine Alternative zu Gradient Descent und dergleichen mit dem großen Vorteil, dass die Aktualisierungen unter vielen Umständen analytisch berechnet werden können. Darüber hinaus ist es ein flexibler Rahmen, um über Optimierung nachzudenken.
In diesem Artikel beginnen wir mit einem einfachen Clustering-Beispiel und diskutieren dann den Algorithmus im Allgemeinen.
Betrachten Sie die Situation, in der Sie eine Vielzahl von Datenpunkten mit einigen Messungen von ihnen haben. Wir wollen sie verschiedenen Gruppen zuordnen.
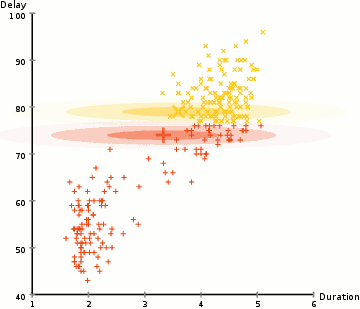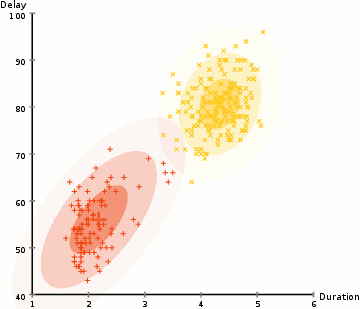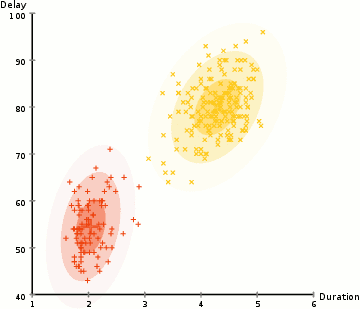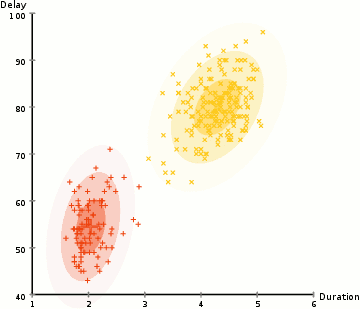
Im Beispiel hier haben wir Daten zu Eruptionen des legendären Old Faithful Geysirs in Yellowstone. Für jeden Ausbruch haben wir seine Länge und die Zeit seit dem vorherigen Ausbruch gemessen. Wir könnten annehmen, dass es zwei „Arten“ von Eruptionen gibt (rot und gelb im Diagramm), und für jede Art von Eruption werden die resultierenden Daten durch eine (multivariate) Normalverteilung generiert. Dies wird übrigens als Gaußsches Mischungsmodell bezeichnet.
Ähnlich wie beim k-Means-Clustering beginnen wir mit einer zufälligen Vermutung für diese beiden Verteilungen / Cluster und verbessern uns dann iterativ, indem wir zwei Schritte abwechseln:
- ( 1) Weisen Sie jeden Datenpunkt probabilistisch einem Cluster zu. In diesem Fall berechnen wir die Wahrscheinlichkeit, dass es aus dem roten Cluster bzw. dem gelben Cluster stammt.
- (Maximierung) Aktualisieren Sie die Parameter für jeden Cluster (gewichtete mittlere Position und Varianz-Kovarianz-Matrix) basierend auf den Punkten im Cluster (gewichtet nach ihrer im ersten Schritt zugewiesenen Wahrscheinlichkeit).
Beachten Sie, dass unser Modell im Gegensatz zum k-Means-Clustering generativ ist: Es gibt vor, uns den Prozess mitzuteilen, durch den die Daten generiert wurden. Und wir könnten wiederum das Modell erneut testen, um mehr (gefälschte) Daten zu generieren.
Verstanden? Jetzt werden wir ein 1-dimensionales Beispiel mit Gleichungen machen.
Betrachten Sie Datenpunkte mit einer einzigen Messung x. Wir nehmen an, dass diese von 2 Clustern erzeugt werden, die jeweils einer Normalverteilung N (μ, σ2) folgen. Die Wahrscheinlichkeit, dass Daten vom ersten Cluster generiert werden, ist π.
Wir haben also 5 Parameter: eine Mischwahrscheinlichkeit π und eine mittlere μ- und Standardabweichung σ für jeden Cluster. Ich werde sie kollektiv als θ bezeichnen.

Wie hoch ist die Wahrscheinlichkeit, einen Datenpunkt mit dem Wert x zu beobachten? Die Wahrscheinlichkeits-Dichte-Funktion der Normalverteilung sei mit ϕ bezeichnet. Um die Notation weniger überladen zu halten, verwende ich die Standardabweichung als Parameter anstelle der üblichen Varianz.

Die Wahrscheinlichkeit (Likelihood), unseren gesamten Datensatz von n Punkten zu beobachten, beträgt:
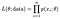
Und wir wählen normalerweise den Logarithmus, um unser Produkt in eine überschaubarere Summe, die Log-Wahrscheinlichkeit, umzuwandeln.

Unser Ziel ist es, dies zu maximieren: Wir möchten, dass unsere Parameter diejenigen sind, bei denen es am wahrscheinlichsten ist, dass wir die von uns beobachteten Daten beobachten (ein Maximum-Likelihood-Schätzer).
Nun ist die Frage, wie werden wir es optimieren? Dies direkt und analytisch zu tun, wäre aufgrund der Summe im Logarithmus schwierig.
Der Trick besteht darin, sich vorzustellen, dass es eine latente Variable gibt, die wir Δ nennen werden. Es ist eine binäre (0/1-wertige) Variable, die bestimmt, ob sich ein Punkt in Cluster 1 oder Cluster 2 befindet. Wenn wir Δ für jeden Punkt kennen, wäre es sehr einfach, die Maximum-Likelihood-Schätzungen unserer Parameter zu berechnen. Um unserer Wahl von Δ als 1 für den zweiten Cluster zu entsprechen, werden wir π auf die Wahrscheinlichkeit umstellen, dass sich ein Punkt im zweiten Cluster befindet.

Beachten Sie, dass die Summen jetzt außerhalb des Logarithmus liegen. Außerdem nehmen wir eine zusätzliche Summe auf, um die Wahrscheinlichkeit zu berücksichtigen, dass wir uns gegenseitig beobachten.
Unter der Annahme, dass wir Δ beobachtet haben, sind die Maximum-Likelihood-Schätzungen leicht zu bilden. Nehmen Sie für μ den Stichprobenmittelwert innerhalb jedes Clusters; für σ ebenfalls die Standardabweichung (die Populationsformel, die der MLE ist). Zum Beispiel der Stichprobenanteil der Punkte im zweiten Cluster. Dies sind die üblichen Maximum-Likelihood-Schätzer für jeden Parameter.
Natürlich haben wir das nicht beobachtet. Die Lösung hierfür ist das Herzstück des Algorithmus zur Erwartungsmaximierung. Unser Plan ist:
- Beginnen Sie mit einer beliebigen anfänglichen Parameterauswahl.
- (Erwartung) Bilden eine Schätzung von Δ.
- (Maximierung) Berechnen Sie die Maximum-Likelihood-Schätzer, um unsere Parameterschätzung zu aktualisieren.
- Wiederholen Sie die Schritte 2 und 3 bis zur Konvergenz.
Auch hier kann es hilfreich sein, über k-Means-Clustering nachzudenken, bei dem wir dasselbe tun. Beim k-Means-Clustering weisen wir jeden Punkt dem nächstgelegenen Schwerpunkt zu (Erwartungsschritt). Im Wesentlichen ist dies eine harte Schätzung von Δ. Schwer, weil es 1 für einen der Cluster und 0 für alle anderen ist. Dann aktualisieren wir die Schwerpunkte auf den Mittelwert der Punkte im Cluster (Maximierungsschritt). Dies ist der Maximum-Likelihood-Schätzer für μ. Beim k-Means-Clustering weist das „Modell“ für die Daten keine Standardabweichung auf. (Das „Modell“ steht in Anführungszeichen, weil es nicht generativ ist).
In unserem Beispiel führen wir stattdessen eine weiche Zuweisung von Δ durch. Wir nennen dies manchmal die Verantwortung (wie verantwortlich ist jeder Cluster für jede Beobachtung). Wir werden die Verantwortung als ɣ bezeichnen.

Jetzt können wir den vollständigen Algorithmus für dieses Beispiel aufschreiben. Aber bevor wir dies tun, werden wir schnell eine Tabelle mit Symbolen überprüfen, die wir definiert haben (es gab viele).

Und hier ist der Algorithmus:

Beachten Sie, dass die Schätzungen von μ und σ für Cluster 1 analog sind, jedoch stattdessen 1–ɣ als Gewichte verwenden.
Nachdem wir nun ein Beispiel für den Algorithmus gegeben haben, haben Sie hoffentlich ein Gefühl dafür. Wir werden den Algorithmus im Allgemeinen diskutieren. Dies läuft im Grunde darauf hinaus, alles, was wir getan haben, mit etwas komplizierteren Variablen zu verkleiden. Und es wird uns in die Lage versetzen zu erklären, warum es funktioniert.
Erwartungsmaximierung im Allgemeinen
Gehen wir zur allgemeinen Einstellung über. Hier ist das Setup:
- Wir haben einige Daten X in welcher Form auch immer.
- Wir setzen voraus, dass es auch unbeobachtete (latente) Daten Δ gibt, wiederum in welcher Form auch immer.
- Wir haben ein Modell mit Parametern θ.
- Wir haben die Möglichkeit, die Log-likelihood ℓ(θ; X, Δ) zu berechnen. Insbesondere das Protokoll der Wahrscheinlichkeit, unsere Daten zu beobachten, und die Zuordnungen der latenten Variablen zu den Parametern.
- Wir haben auch die Möglichkeit, das Modell zu verwenden, um die bedingte Verteilung Δ | X bei einer Reihe von Parametern zu berechnen. Wir werden dieses P (Δ | X; θ) bezeichnen.
- Folglich können wir die Log-likelihood ℓ(θ; X) berechnen. Dies ist das Protokoll der Wahrscheinlichkeit, unsere Daten bei gegebenen Parametern zu beobachten (ohne eine Zuordnung für die latenten Variablen anzunehmen).
Mit P, um die Wahrscheinlichkeit zu bezeichnen, können wir jetzt die Kettenregel verwenden, um zu schreiben:

Die Notation finden Sie hier. Alle drei Terme nehmen die Parameter θ als gegeben an.
- Der erste Term links ist die Beobachtungswahrscheinlichkeit der Daten und eine vorgegebene latente Variablenzuordnung.
- Der erste Term auf der rechten Seite ist die Wahrscheinlichkeit der angegebenen Zuordnung der latenten Variablen bei den beobachteten Daten.
- Der letzte Term ist die Wahrscheinlichkeit, die Daten zu beobachten.
Wir können Logarithmen nehmen und Terme neu anordnen. Dann werden wir in der zweiten Zeile eine Notationsänderung vornehmen (und zwar eine verwirrende. Gib mir keine Schuld, ich habe es nicht erfunden):
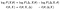
Für die ersten beiden Begriffe lohnt es sich zu überprüfen, was sie im Kontext unseres vorherigen Beispiels sind. Das erste, ℓ(θ; X), ist dasjenige, das wir optimieren möchten. Das zweite, ℓ (θ; X, Δ), war dasjenige, das analytisch handhabbar war.
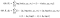
Denken Sie nun daran, dass ich gesagt habe, wir können die bedingte Verteilung Δ | X unter Berücksichtigung der Parameter θ berechnen? Dies ist, wo die Dinge wild.
Wir werden einen zweiten Satz derselben Parameter einführen, nennen wir ihn θʹ. Ich werde es manchmal auch mit einem Hut (Circumflex) darüber bezeichnen, wie der, den dieses „Hemd“ hat.2 Stellen Sie sich diesen Parametersatz als unsere aktuelle Schätzung vor. Die derzeit in unseren Formeln enthaltenen Daten werden optimiert, um unsere Schätzung zu verbessern.
Nun nehmen wir die Erwartung der Log–Wahrscheinlichkeiten in Bezug auf die bedingte Verteilung Δ | X, θʹ – nämlich die Verteilung unserer latenten Variablen angesichts der Daten und unserer aktuellen Parameterschätzung.

Der Begriff auf der linken Seite ändert sich nicht, da er Δ sowieso nicht kennt / interessiert (es ist eine Konstante). Auch hier liegt die Erwartung über den möglichen Werten von Δ. Wenn Sie in Bezug auf unser Beispiel folgen, ändert sich der Begriff ℓ(θ; X, Δ), nachdem wir die Erwartung genommen haben, so dass Δ durch ɣ ersetzt wird.

Nun, sehr schnell, um den notationalen Albtraum, den wir hier haben, zu verbessern, lassen Sie uns die Kurznotation für die beiden Erwartungen einführen, die wir auf der rechten Seite haben
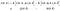
Der Algorithmus wird:

Warum es funktioniert
Das schwere Heben, um zu beweisen, dass dies funktioniert, besteht darin, die Funktion R(θ, θʹ) zu betrachten. Die Behauptung ist, dass R maximiert wird, wenn θ=θʹ . Denken wir anstelle eines vollständigen Beweises darüber nach, was R berechnet. Wenn man die Abhängigkeit von den Daten X (die zwischen der Verteilung, über die wir eine Erwartung nehmen, und der Wahrscheinlichkeitsfunktion geteilt werden) entfernt, wird R schematisch

Mit anderen Worten, wir haben zwei Wahrscheinlichkeitsverteilungen. Wir verwenden einen (parametrisiert durch θʹ), um Daten Δ zu generieren, und wir verwenden den anderen (parametrisiert durch θ), um die Wahrscheinlichkeit dessen zu berechnen, was wir gesehen haben. Wenn Δ nur eine einzelne Zahl darstellt und die Verteilungen Wahrscheinlichkeitsdichtefunktionen haben, könnten wir schreiben (wiederum schematisch)
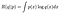
Ich habe dies suggestiv in einer ähnlichen Form wie die Kullback-Leibler (KL) -Divergenz geschrieben, die (fast) ein Maß für den Abstand zwischen zwei Wahrscheinlichkeitsverteilungen ist. Wenn wir R(q ||p) von einer Konstanten R(p ||p) subtrahieren, erhalten wir die KL-Divergenz, die unten bei 0 begrenzt ist und nur 0 ist, wenn q=p. (Das einzige, was eine Distanz3 0 von der Verteilung p ist, ist p selbst). Mit anderen Worten, R wird maximiert, wenn q= p. Dies ist ein Standardergebnis über die KL-Divergenz und kann mit der Jensen-Ungleichung bewiesen werden.⁴
Jetzt müssen Sie nur noch den Unterschied zwischen den Wahrscheinlichkeiten vor und nach unserem Update-Schritt berücksichtigen:

Wir haben die neuen Parameter ausgewählt, um Q zu maximieren, sodass der erste Term definitiv positiv ist. Mit dem obigen Argument wird R maximiert, indem die alten Parameter als erstes Argument verwendet werden, sodass der zweite Term negativ sein muss. Positiv minus negativ ist positiv. Daher ist die Wahrscheinlichkeit bei jedem Aktualisierungsschritt gestiegen. Jeder Schritt macht die Dinge garantiert besser.
Beachten Sie auch, dass wir Q nicht optimieren müssen. Wir müssen nur einen Weg finden, es besser zu machen, und unsere Updates werden die Dinge immer noch garantiert verbessern.
Fazit
Hoffentlich haben Sie jetzt ein gutes Gefühl für den Algorithmus. In Bezug auf die Mathematik ist die Schlüsselgleichung nur die Wahrscheinlichkeiten unten. Danach nehmen wir nur die Erwartungen in Bezug auf die alten Parameter (den Erwartungsschritt) und zeigen, dass es uns gut geht, nur den ersten Term auf der rechten Seite zu optimieren. Wie wir am Beispiel des Gaußschen Mischungsmodells gesehen haben, ist dieser zweite Term oft einfacher zu optimieren. Die dritte Amtszeit müssen wir uns keine Sorgen machen, es wird nichts durcheinander bringen.
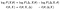
Wenn ich ein wenig zurücktrete, möchte ich die Leistungsfähigkeit und Nützlichkeit des EM-Algorithmus betonen. Zunächst stellt es die Idee dar, dass wir latente Variablen einführen und dann berechnen können, indem wir abwechselnd mit den latenten Variablen (wobei die Parameter als fest und bekannt gelten) und mit den Parametern (wobei die latenten Variablen als fest und bekannt gelten) umgehen. Dies ist eine starke Idee, die Sie in einer Vielzahl von Kontexten sehen werden.
Zweitens ist der Algorithmus inhärent schnell, da er nicht von der Berechnung von Gradienten abhängt. Jedes Mal, wenn Sie ein Modell analytisch lösen können (z. B. mithilfe einer linearen Regression), wird es schneller. Und das ermöglicht es uns, analytisch unlösbare Probleme zu nehmen und Teile von ihnen analytisch zu lösen und diese Kraft auf einen iterativen Kontext auszudehnen.
Abschließend möchte ich anmerken, dass es noch viel mehr über den EM-Algorithmus zu sagen gibt. Es verallgemeinert sich auf andere Formen des Maximierungsschrittes und auf variationelle Bayes’sche Techniken und kann auf unterschiedliche Weise verstanden werden (zum Beispiel als Maximierung-Maximierung oder als alternierende Projektionen auf eine Submanifold unter gegenseitig dualen affinen Verbindungen auf einer statistischen Mannigfaltigkeit (die e- und m-Verbindungen)). Mehr dazu in der Zukunft!