Spiegazione della massimizzazione delle aspettative

Expectation Maximization (EM) è un algoritmo classico sviluppato negli anni ’60 e’ 70 con diverse applicazioni. Può essere utilizzato come algoritmo di clustering non supervisionato e si estende ad applicazioni NLP come Latent Dirichlet Allocation1, l’algoritmo Baum–Welch per i modelli nascosti di Markov e l’imaging medico. Come procedura di ottimizzazione, è un’alternativa alla discesa del gradiente e simili con il vantaggio principale che, in molte circostanze, gli aggiornamenti possono essere calcolati analiticamente. Inoltre, è un framework flessibile per pensare all’ottimizzazione.

In questo articolo, inizieremo con un semplice esempio di clustering e poi discuteremo l’algoritmo in generale.

Considera la situazione in cui hai una varietà di punti dati con alcune misurazioni di essi. Desideriamo assegnarli a diversi gruppi.

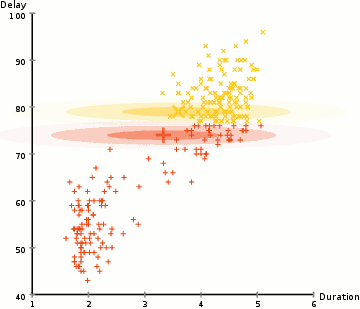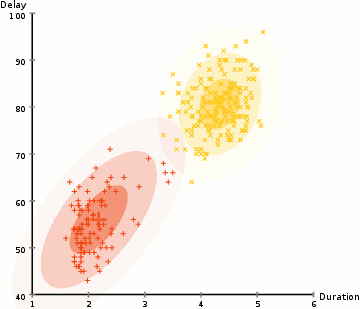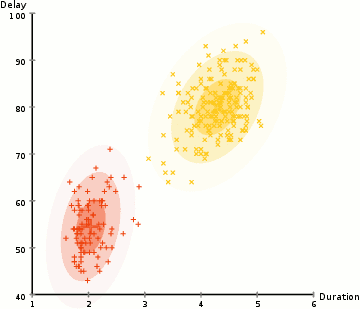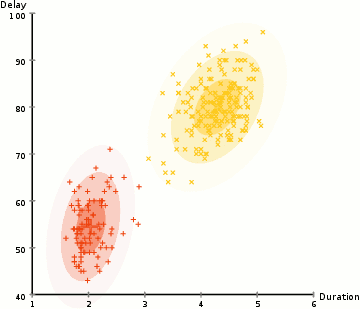
Nell’esempio qui abbiamo dati sulle eruzioni dell’iconico Vecchio geyser fedele a Yellowstone. Per ogni eruzione, abbiamo misurato la sua lunghezza e il tempo dall’eruzione precedente. Potremmo supporre che ci siano due” tipi ” di eruzioni (rosso e giallo nel diagramma), e per ogni tipo di eruzione i dati risultanti sono generati da una distribuzione normale (multivariata). Questo è chiamato un modello di miscela gaussiana, incidentalmente.

Simile a k-means clustering, iniziamo con un’ipotesi casuale per cosa sono queste due distribuzioni / cluster e quindi procediamo a migliorare iterativamente alternando due passaggi:

1. (Aspettativa) Assegnare ogni punto dati a un cluster in modo probabilistico. In questo caso, calcoliamo la probabilità che provenga rispettivamente dal cluster rosso e dal cluster giallo.
2. (Massimizzazione) Aggiorna i parametri per ciascun cluster (posizione media ponderata e matrice varianza-covarianza) in base ai punti del cluster (ponderati per la loro probabilità assegnata nel primo passaggio).

Si noti che a differenza di k-means clustering, il nostro modello è generativo: pretende di dirci il processo con cui i dati sono stati generati. E potremmo, a sua volta, ri-campionare il modello per generare più dati (falsi).

Capito? Ora faremo un esempio 1-dimensionale con equazioni.

Considera i punti dati con una singola misura x. Supponiamo che questi siano generati da 2 cluster ciascuno seguendo una distribuzione normale N(μ, σ2). La probabilità che i dati vengano generati dal primo cluster è π.

Quindi abbiamo 5 parametri: una probabilità di miscelazione π, e una media μ e deviazione standard σ per ogni cluster. Li denoterò collettivamente come θ.

Qual è la probabilità di osservare un datapoint con valore di x? Lascia che la funzione di densità di probabilità della distribuzione normale sia denotata da ϕ. Per mantenere la notazione meno ingombra, userò la deviazione standard come parametro invece della solita varianza.

La probabilità (probabilità) di osservare il nostro intero set di dati, di n punti è:

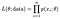
E noi di solito scegliere di prendere il logaritmo di questo per trasformare il nostro prodotto in un più gestibile somma, la log-verosimiglianza.

il Nostro obiettivo è quello di massimizzare questo: vogliamo che i nostri parametri da quelli in cui è più probabile che osserviamo i dati osservati (uno Stimatore di Massima Verosimiglianza).

Ora la domanda è: come lo ottimizzeremo? Farlo direttamente e analiticamente sarebbe complicato a causa della somma nel logaritmo.

Il trucco è immaginare che ci sia una variabile latente che chiameremo Δ. È una variabile binaria (con valore 0/1) che determina se un punto si trova nel cluster 1 o nel cluster 2. Se conosciamo Δ per ogni punto, sarebbe molto facile calcolare le stime di massima verosimiglianza dei nostri parametri. Per comodità di abbinare la nostra scelta di Δ essere 1 per il secondo cluster, cambieremo π per essere la probabilità che un punto sia nel secondo cluster.

Si noti che le somme sono ora al di fuori del logaritmo. Inoltre, raccogliamo una somma extra per tenere conto della probabilità di osservare ogni Δ.

Supponendo controfattualmente che abbiamo osservato Δ, le stime di massima verosimiglianza sono facili da formare. Per μ, prendi la media del campione all’interno di ciascun cluster; per σ, allo stesso modo la deviazione standard (la formula della popolazione, che è il MLE). Per π, la proporzione campione di punti nel secondo cluster. Questi sono i soliti stimatori di massima verosimiglianza per ciascun parametro.

Naturalmente, non abbiamo osservato Δ. La soluzione a questo è il cuore dell’algoritmo di massimizzazione delle aspettative. Il nostro piano è:

1. Inizia con una scelta iniziale arbitraria di parametri.
2. (Aspettativa) Formano una stima di Δ.
3. (Massimizzazione) Calcola gli stimatori di massima verosimiglianza per aggiornare la nostra stima dei parametri.
4. Ripetere i passaggi 2 e 3 alla convergenza.

Di nuovo, potresti trovare utile pensare al clustering di k-means, dove facciamo la stessa cosa. In k-means clustering, assegniamo ogni punto al centroide più vicino (passo di aspettativa). In sostanza, questa è una stima difficile di Δ. Difficile perché è 1 per uno dei cluster e 0 per tutti gli altri. Quindi aggiorniamo i centroidi per essere la media dei punti nel cluster (fase di massimizzazione). Questo è lo stimatore di massima verosimiglianza per μ. In k-means clustering, il “modello” per i dati non ha una deviazione standard. (Il “modello” è tra virgolette spaventose perché non è generativo).

Nel nostro esempio, faremo invece un’assegnazione morbida di Δ. A volte chiamiamo questa responsabilità (quanto è responsabile ogni cluster per ogni osservazione). Denoteremo la responsabilità come ɣ.

Ora possiamo scrivere l’algoritmo completo per questo esempio. Ma prima di farlo, esamineremo rapidamente una tabella di simboli che abbiamo definito (ce n’erano molti).

Ed ecco l’algoritmo:

Si noti che le stime di μ e σ per il cluster 1 sono analoghe ma utilizzano invece 1–ɣ come pesi.

Ora che abbiamo dato un esempio dell’algoritmo, si spera di averne un’idea. Passeremo a discutere l’algoritmo in generale. Questo equivale fondamentalmente a vestire tutto ciò che abbiamo fatto con variabili leggermente più complicate. E ci metterà in grado di spiegare perché funziona.

Massimizzazione delle aspettative in generale

Passiamo all’impostazione generale. Ecco la configurazione:

1. Abbiamo alcuni dati X di qualsiasi forma.
2. Supponiamo che ci siano anche dati non osservati (latenti) Δ, di nuovo di qualsiasi forma.
3. Abbiamo un modello con parametri θ.
4. Abbiamo la capacità di calcolare la probabilità di log ℓ(θ; X, Δ). In particolare, il registro della probabilità di osservare i nostri dati e le assegnazioni specificate delle variabili latenti dati i parametri.
5. Abbiamo anche la possibilità di utilizzare il modello per calcolare la distribuzione condizionale Δ|X dato un insieme di parametri. Denoteremo questo P (Δ|X; θ).
6. Di conseguenza possiamo calcolare la probabilità di log ℓ (θ; X). Questo è il registro della probabilità di osservare i nostri dati dati i parametri (senza assumere un incarico per le variabili latenti).

Usando P per indicare la probabilità, ora possiamo usare la regola della catena per scrivere:

La notazione può essere sottile qui. Tutti e tre i termini prendono i parametri θ come un dato.

1. Il primo termine a sinistra è la probabilità di osservare i dati e un’assegnazione variabile latente specificata.
2. Il primo termine sul lato destro è la probabilità dell’assegnazione specificata delle variabili latenti dati i dati osservati.
3. L’ultimo termine è la probabilità di osservare i dati.

Possiamo prendere logaritmi e riorganizzare i termini. Quindi nella seconda riga faremo un cambiamento di notazione (e uno confuso a quello. Non incolpare me, non l’ho inventato io):

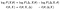
Per i primi due termini, vale la pena rivedere ciò che sono nel contesto del nostro esempio precedente. Il primo, θ (θ; X), è quello che vogliamo ottimizzare. Il secondo, θ (θ; X, Δ), era quello che era analiticamente trattabile.

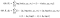
Ora, ricorda che ho detto che possiamo calcolare la distribuzione condizionale Δ / X dati i parametri θ? Questo è dove le cose si scatenano.

Stiamo per introdurre un secondo insieme degli stessi parametri, chiamarlo θʹ. A volte lo denoterò anche con un cappello (circonflesso) sopra di esso, come quello che questo “ê” ha.2 Pensate a questo insieme di parametri come la nostra stima corrente. Il θ attualmente nelle nostre formule sarà ottimizzato per migliorare la nostra stima.

Ora prendiamo l’aspettativa delle probabilità di log rispetto alla distribuzione condizionale Δ|X, θ namely – vale a dire, la distribuzione delle nostre variabili latenti dati i dati e la nostra stima dei parametri attuali.

Il termine sul lato sinistro non cambia poiché non sa/si preoccupa comunque di Δ (è una costante). Ancora una volta, l’aspettativa è sopra i possibili valori di Δ. Se stai seguendo rispetto al nostro esempio, il termine ℓ(θ; X, Δ) cambia dopo aver preso l’aspettativa in modo che Δ sia sostituito da ɣ.

Ora, molto velocemente, per migliorare la notazione incubo abbiamo qui, introduciamo la notazione abbreviata per la due le aspettative che abbiamo sul lato destro

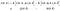
L’algoritmo diventa:

Perché funziona

Il lavoro pesante per dimostrare che funzionerà è considerare la funzione R(θ, θʹ). L’affermazione è che R è massimizzato quando θ = θʹ. Al posto di una prova completa pensiamo a cosa calcola R. Togliendo la dipendenza dalla data X (che è condiviso tra la distribuzione si stanno prendendo delle aspettative e la funzione di verosimiglianza), R schematicamente diventa

In altre parole, abbiamo due distribuzioni di probabilità. Usiamo uno (parametrizzato da θʹ) per generare dati Δ e usiamo l’altro (parametrizzato da θ) per calcolare la probabilità di ciò che abbiamo visto. Se Δ rappresenta un numero unico e le distribuzioni hanno probabilità di funzioni di densità, si può scrivere (di nuovo, schematicamente)

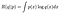
ho suggestivamente scritto questo in una forma simile a quella di Kullback-Leibler (KL) Divergenza che è (quasi) una misura della distanza tra due distribuzioni di probabilità. Se sottraiamo R(q||p) da una costante R (p||p) otterremo la divergenza KL che è limitata sotto a 0 ed è solo 0 quando q=p. (L’unica cosa a distance3 0 dalla distribuzione p è p stessa). In altre parole, R è massimizzato quando q = p. Questo è un risultato standard sulla divergenza KL e può essere dimostrato con la disuguaglianza di Jensen.Now

Ora l’unica cosa da fare è considerare la differenza tra le probabilità prima e dopo il nostro passaggio di aggiornamento:

Abbiamo scelto i nuovi parametri per massimizzare Q, quindi il primo termine è decisamente positivo. Con l’argomento sopra, R viene massimizzato prendendo i vecchi parametri come primo argomento, quindi il secondo termine deve essere negativo. Positivo meno negativo è positivo. Pertanto la probabilità è aumentata ad ogni passaggio di aggiornamento. Ogni passo è garantito per rendere le cose migliori.

Si noti inoltre che non è necessario ottimizzare Q. Tutto quello che dobbiamo è trovare un modo per renderlo migliore e i nostri aggiornamenti sono ancora garantiti per migliorare le cose.

Conclusione

Si spera che ora si abbia una buona sensazione per l’algoritmo. In termini di matematica, l’equazione chiave è solo la probabilità di seguito. Dopodiché, prendiamo solo le aspettative rispetto ai vecchi parametri (il passo delle aspettative) e mostriamo che stiamo bene per ottimizzare solo il primo termine sul lato destro. Come abbiamo motivato con l’esempio del modello di miscela gaussiana, questo secondo termine è spesso più facile da ottimizzare. Il terzo mandato di cui non dobbiamo preoccuparci, non rovinerà nulla.

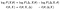
Facendo un passo indietro, voglio sottolineare la potenza e l’utilità dell’algoritmo EM. Prima di tutto, rappresenta l’idea che possiamo introdurre variabili latenti e quindi calcolare trattando alternativamente le variabili latenti (prendendo i parametri come fissi e noti) e trattando i parametri (prendendo le variabili latenti come fissi e noti). Questa è un’idea potente che vedrai in una varietà di contesti.

In secondo luogo, l’algoritmo è intrinsecamente veloce perché non dipende dai gradienti di calcolo. Ogni volta che puoi risolvere un modello analiticamente (come usare una regressione lineare), sarà più veloce. E questo ci permette di prendere problemi analiticamente intrattabili e risolvere parti di essi analiticamente, estendendo quel potere a un contesto iterativo.

Infine, voglio sottolineare che c’è molto altro da dire sull’algoritmo EM. Si generalizza ad altre forme di fare la fase di massimizzazione e alle tecniche bayesiane variazionali e può essere inteso in modi diversi (ad esempio come massimizzazione-massimizzazione o come proiezioni alternate a un submanifold sotto connessioni affine reciprocamente duali su un collettore statistico (le connessioni e – e m)). Più su che in futuro!