Verwachtingsmaximalisatie uitgelegd

Expectation Maximization (EM) is een klassiek algoritme ontwikkeld in de jaren 60 en 70 met diverse toepassingen. Het kan worden gebruikt als een unsupervised clustering algoritme en strekt zich uit tot NLP toepassingen zoals latente Dirichlet Allocation1, het Baum–Welch algoritme voor verborgen Markov modellen, en medische beeldvorming. Als optimalisatieprocedure is het een alternatief voor gradiëntafdaling en dergelijke met het grote voordeel dat de updates in veel omstandigheden analytisch kunnen worden berekend. Meer dan dat, het is een flexibel kader voor het denken over optimalisatie.

In dit artikel beginnen we met een eenvoudig clustering voorbeeld en bespreken we het algoritme in het algemeen.

overweeg de situatie waarin u een verscheidenheid aan datapunten hebt met enkele metingen ervan. We willen ze aan verschillende groepen toewijzen.

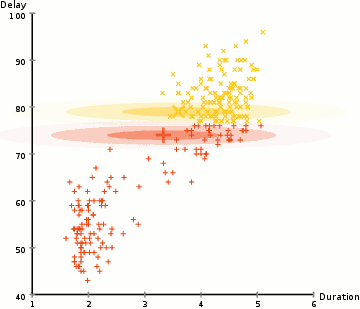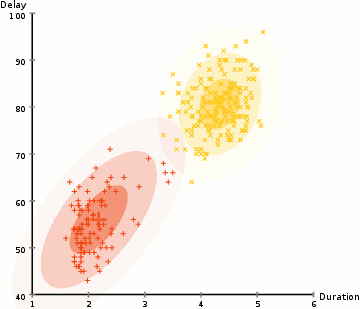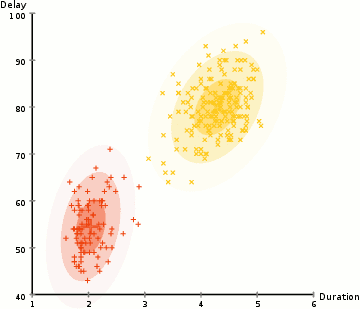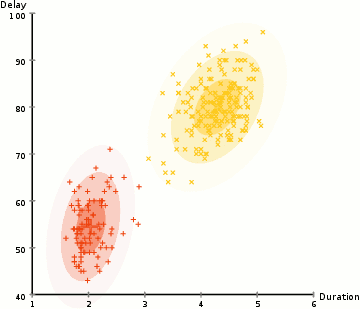
in het voorbeeld hier hebben we gegevens over uitbarstingen van de iconische oude trouwe geiser in Yellowstone. Voor elke uitbarsting hebben we de lengte gemeten en de tijd sinds de vorige uitbarsting. We zouden kunnen veronderstellen dat er twee “types” van uitbarstingen (rood en geel in het diagram), en voor elk type van uitbarsting de resulterende gegevens worden gegenereerd door een (multivariate) normale verdeling. Dit heet overigens een Gaussiaans Mengmodel.

vergelijkbaar met k-means clustering, beginnen we met een willekeurige gok voor wat die twee distributies/clusters zijn en gaan we vervolgens verder om iteratief te verbeteren door twee stappen af te wisselen:

1. (verwachting) toewijzen elk gegevenspunt aan een cluster probabilistically. In dit geval berekenen we de waarschijnlijkheid dat het uit respectievelijk de rode en de gele cluster kwam.
2. (maximalisatie) actualiseer de parameters voor elke cluster (gewogen gemiddelde locatie en variantie-covariantiematrix) op basis van de punten in de cluster (gewogen met hun waarschijnlijkheid toegewezen in de eerste stap).

merk op dat in tegenstelling tot in k-means clustering, Ons model generatief is: het beweert ons het proces te vertellen waardoor de gegevens werden gegenereerd. En we zouden op onze beurt het model opnieuw kunnen sampleen om meer (valse) gegevens te genereren.

heb je het? Nu gaan we een 1-dimensionaal voorbeeld doen met vergelijkingen.

beschouw gegevenspunten met een enkele meting x. we veronderstellen dat deze worden gegenereerd door 2 clusters die elk een normale verdeling N(μ, σ2) volgen. De waarschijnlijkheid van gegevens die door de eerste cluster worden gegenereerd is π.

dus we hebben 5 parameters: een mengkans π, en een gemiddelde μ en standaardafwijking σ voor elke cluster. Ik zal ze gezamenlijk aanduiden als θ.

Wat is de waarschijnlijkheid van het waarnemen van een datapunt met waarde x? Laat de kans-dichtheidsfunctie van de normale verdeling worden aangeduid met ϕ. Om notatie minder rommelig te houden, zal ik de standaarddeviatie als parameter gebruiken in plaats van de gebruikelijke variantie.

De waarschijnlijkheid (kans) van het observeren van onze gehele dataset van n punten is:

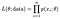
En we meestal voor kiezen om de logaritme van deze in te schakelen ons product naar een meer beheersbaar som, de log-likelihood.

ons doel is om dit te maximaliseren: we willen dat onze parameters degenen zijn waar het meest waarschijnlijk is dat we de waargenomen gegevens observeren (een maximale waarschijnlijkheid Estimator).

nu is de vraag: hoe gaan we het optimaliseren? Dit direct en analytisch doen zou lastig zijn vanwege de som in de logaritme.

de truc is om je voor te stellen dat er een latente variabele is die we Δ zullen noemen. Het is een binaire variabele (0/1-waarde) die bepaalt of een punt zich in cluster 1 of cluster 2 bevindt. Als we Δ voor elk punt kennen, zou het heel gemakkelijk zijn om de schattingen van de maximale waarschijnlijkheid van onze parameters te berekenen. Voor het gemak om onze keuze aan te passen van Δ Die 1 voor de tweede cluster zijn, zullen wij π omschakelen om de waarschijnlijkheid te zijn van een punt dat in de tweede cluster is.

merk op dat de sommen nu buiten de logaritme liggen. Ook halen we een extra som op om rekening te houden met de waarschijnlijkheid van het waarnemen van elke Δ.

stel dat we Δ hebben waargenomen, dan zijn de maximale waarschijnlijkheidsschattingen gemakkelijk te maken. Neem Voor μ het steekproefgemiddelde binnen elke cluster; voor σ eveneens de standaardafwijking (de populatieformule, die de MLE is). Voor π, de steekproefverhouding van de punten in de tweede cluster. Dit zijn de gebruikelijke maximale waarschijnlijkheidsinschattingen voor elke parameter.

natuurlijk hebben we Δ niet waargenomen. De oplossing hiervoor is het hart van het Verwachtingsmaximalisatiealgoritme. Ons plan is:

1. begin met een willekeurige initiële keuze van parameters.
2. (verwachting) vormen een schatting van Δ.
3. (maximalisatie) Bereken de maximale waarschijnlijkheid schatters om onze parameterschatting bij te werken.
4. Herhaal stap 2 en 3 voor convergentie.

nogmaals, u kunt het nuttig vinden om na te denken over K-betekent clustering, waar we hetzelfde doen. In k-means clustering wijzen we elk punt toe aan de dichtstbijzijnde centroid (verwachting stap). In wezen is dit een harde schatting van Δ. Moeilijk, want het is 1 voor een van de clusters en 0 voor alle andere. Vervolgens werken we de centroids bij om het gemiddelde van de punten in de cluster te zijn (maximalisatiestap). Dit is de maximale waarschijnlijkheid estimator Voor μ. In k-betekent clustering, het” model ” voor de gegevens heeft geen standaardafwijking. (Het “model” staat in schrikcitaten omdat het niet generatief is).

in ons voorbeeld doen we in plaats daarvan een zachte toewijzing van Δ. We noemen dit soms de verantwoordelijkheid (hoe verantwoordelijk is elke cluster voor elke waarneming). Wij zullen de verantwoordelijkheid Als ɣ aanduiden.

nu kunnen we het volledige algoritme voor dit voorbeeld opschrijven. Maar voordat we dit doen, zullen we snel een tabel met symbolen die we hebben gedefinieerd bekijken (Er waren veel).

en hier is het algoritme:

merk op dat de schattingen van μ en σ Voor cluster 1 analoog zijn, maar in plaats daarvan 1–ɣ als de gewichten gebruiken.

nu we een voorbeeld van het algoritme hebben gegeven, heb je er hopelijk gevoel voor. We gaan verder met het bespreken van het algoritme in het algemeen. Dit komt neer op het verkleden van alles wat we deden met iets meer gecompliceerde variabelen. En het zal ons in staat stellen om uit te leggen waarom het werkt.

Verwachtingsmaximalisatie in het algemeen

laten we naar de Algemene instelling gaan. Hier is de setup:

1. we hebben wat data X van welke vorm dan ook.
2. we stellen vast dat er ook niet geobserveerde (latente) gegevens Δ zijn, ook in welke vorm dan ook.
3. we hebben een model met parameters θ.
4. we hebben de mogelijkheid om de log-waarschijnlijkheid te berekenen, j(θ; X, Δ). Specifiek, de log van de waarschijnlijkheid van het observeren van onze gegevens en gespecificeerde toewijzingen van de latente variabelen gegeven de parameters.
5. we hebben ook de mogelijkheid om het model te gebruiken om de voorwaardelijke verdeling Δ|X te berekenen gegeven een reeks parameters. We zullen deze P(Δ|X; θ) aangeven.
6. als gevolg hiervan kunnen we de log-waarschijnlijkheid formula_3(θ; X) berekenen. Dit is de log van de waarschijnlijkheid van het observeren van onze gegevens gegeven de parameters (zonder het aannemen van een toewijzing voor de latente variabelen).

met behulp van P om de waarschijnlijkheid aan te geven, kunnen we nu de kettingregel gebruiken om te schrijven:

de notatie kan hier subtiel zijn. Alle drie termen nemen de parameters θ als een gegeven.

1. de eerste term links is de waarschijnlijkheid van het waarnemen van de gegevens en een gespecificeerde latente variabele toewijzing.
2. de eerste term aan de rechterkant is de waarschijnlijkheid van de gespecificeerde toewijzing van de latente variabelen gegeven de waargenomen gegevens.
3. de laatste term is de waarschijnlijkheid dat de gegevens worden waargenomen.

we kunnen logaritmen nemen en termen herschikken. Dan in de tweede regel zullen we een notatie verandering (en een verwarrende een op dat. Geef mij niet de schuld, Ik heb het niet uitgevonden.):

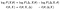
voor de eerste twee termen is het de moeite waard om te bekijken wat ze zijn in de context van ons vorige voorbeeld. De eerste, δ (θ; X), is degene die we willen optimaliseren. De tweede, δ (θ; X, Δ), was degene die analytisch tracteerbaar was.

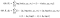
nu, weet je nog dat ik zei dat we de voorwaardelijke verdeling Δ|X kunnen berekenen gegeven de parameters θ? Dit is waar het wild wordt.

we gaan een tweede set van dezelfde parameters introduceren, noem het θʹ. Ik zal het ook soms aanduiden met een hoed (circumflex) eroverheen, zoals deze “ê” heeft.2 Denk aan deze set parameters als onze huidige schatting. De θ die momenteel in onze formules wordt geoptimaliseerd om onze schatting te verbeteren.

nu gaan we de verwachting van de log likelihoods nemen met betrekking tot de voorwaardelijke verdeling Δ|X, θʹ – namelijk, de verdeling van onze latente variabelen gegeven de gegevens en onze huidige parameterschatting.

de term aan de linkerkant verandert niet omdat het niet weet/Zorg Over Δ anyways (het is een constante). Nogmaals, de verwachting is over de mogelijke waarden van Δ. Als je ons voorbeeld volgt, verandert de term δ (θ; X, Δ) nadat we de verwachting hebben genomen zodat Δ wordt vervangen door ɣ.

nu, heel snel, om de notatie nachtmerrie die we hier hebben te verlichten, laten we de steno notatie introduceren voor de twee verwachtingen die we aan de rechterkant hebben

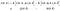
het algoritme wordt:

waarom het werkt

het zware tillen om te bewijzen dat dit zal werken is de functie R(θ, θʹ) te overwegen. De claim is dat R wordt gemaximaliseerd wanneer θ = θʹ. In plaats van een volledig bewijs laten we nadenken over wat R berekent. Door de afhankelijkheid van de data X (die wordt gedeeld tussen de distributie die we een verwachting over nemen en de waarschijnlijkheidsfunctie) weg te halen, wordt r schematisch

met andere woorden, we hebben twee kansverdelingen. We gebruiken een (geparametreerd door θʹ) om data Δ te genereren en we gebruiken de andere (geparametreerd door θ) om de waarschijnlijkheid van wat we zagen te berekenen. Als Δ slechts een enkel getal vertegenwoordigt en de verdelingen kans-dichtheidsfuncties hebben, kunnen we (opnieuw, schematisch)

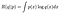
ik heb dit suggestief geschreven in een vorm vergelijkbaar met die van de divergentie Kullback-Leibler (KL) die (bijna) een maat is voor de afstand tussen twee kansverdelingen. Als we R(q||p) aftrekken van een constante R(p||p) krijgen we de KL-divergentie die onder 0 wordt begrensd en slechts 0 is wanneer q=p. (het enige dat een afstand3 0 van de verdeling p is P zelf). Met andere woorden, R wordt gemaximaliseerd wanneer q=p. Dit is een standaard resultaat over de KL-divergentie en kan worden bewezen met Jensen ongelijkheid.⁴

nu is het enige wat we nog moeten doen het verschil tussen de waarschijnlijkheden voor en na onze update stap overwegen:

we kozen de nieuwe parameters om Q te maximaliseren, dus de eerste term is zeker positief. Door het bovenstaande argument wordt R gemaximaliseerd door de oude parameters als eerste argument te nemen, dus de tweede term moet negatief zijn. Positief min negatief is positief. Daarom is de waarschijnlijkheid bij elke update stap toegenomen. Elke stap is gegarandeerd om dingen beter te maken.

merk ook op dat we Q niet hoeven te optimaliseren. Alles wat we moeten vinden is een manier om het beter te maken en onze updates zijn nog steeds gegarandeerd om dingen beter te maken.

conclusie

hopelijk heb je nu een goed gevoel voor het algoritme. In termen van de wiskunde, de belangrijkste vergelijking is gewoon de waarschijnlijkheden hieronder. Daarna nemen we gewoon verwachtingen ten opzichte van de oude parameters (de verwachting stap) en laten zien dat we het prima vinden om gewoon de eerste term aan de rechterkant te optimaliseren. Omdat we motiveerden met het Gaussiaanse Mengmodel voorbeeld, is deze tweede term vaak makkelijker te optimaliseren. De derde termijn waar we ons geen zorgen over hoeven te maken, zal niets verpesten.

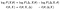
even een stapje terug, wil ik de kracht en het nut van het EM-algoritme benadrukken. Allereerst, het vertegenwoordigt het idee dat we latente variabelen kunnen introduceren en vervolgens berekenen door afwisselend omgaan met de latente variabelen (waarbij de parameters als vast en bekend) en omgaan met de parameters (waarbij de latente variabelen als vast en bekend). Dit is een krachtig idee dat je in verschillende contexten zult zien.

ten tweede is het algoritme inherent snel omdat het niet afhankelijk is van het berekenen van gradiënten. Wanneer je een model analytisch kunt oplossen (zoals het gebruik van een lineaire regressie), gaat het sneller. Dit laat ons analytisch hardnekkige problemen nemen en delen ervan analytisch oplossen, en die kracht uitbreiden naar een iteratieve context.

tot slot wil ik opmerken dat er nog veel meer te zeggen is over het EM algoritme. Het veralgemeent aan andere vormen van het doen van de maximalisatiestap en aan variationele Bayesiaanse technieken en kan op verschillende manieren worden begrepen (bijvoorbeeld als maximalisatie-maximalisatie of als afwisselende projecties aan een submanifold onder wederzijds dubbele affiene verbindingen op een statistische variëteit (de e – en m – verbindingen)). Meer daarover in de toekomst!