forventning maksimering forklaret

Forventningsmaksimering (EM) er en klassisk algoritme udviklet i 60 ‘erne og 70’ erne med forskellige applikationer. Det kan bruges som en uovervåget klyngealgoritme og strækker sig til NLP–applikationer som Latent Dirichlet Allocation1, Baum-Velch-algoritmen til skjulte Markov-modeller og medicinsk billeddannelse. Som en optimeringsprocedure er det et alternativ til gradientafstamning og lignende med den største fordel, at opdateringerne under mange omstændigheder kan beregnes analytisk. Mere end det er det en fleksibel ramme for at tænke på optimering.

i denne artikel starter vi med et simpelt klyngeeksempel og diskuterer derefter algoritmen generelt.

overvej situationen, hvor du har en række datapunkter med nogle målinger af dem. Vi ønsker at tildele dem til forskellige grupper.

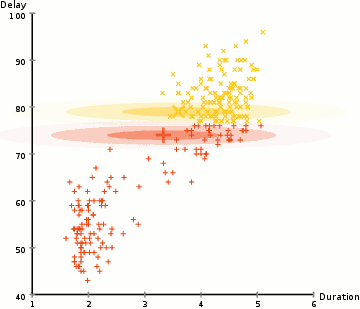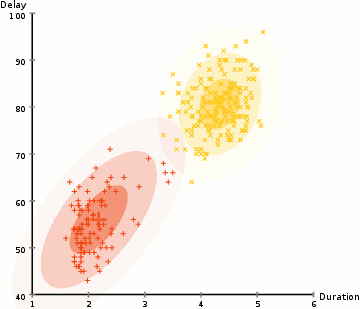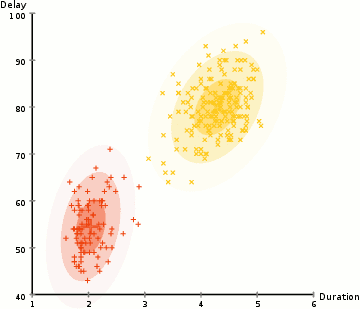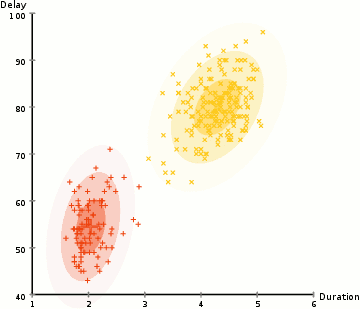
i eksemplet her har vi data om udbrud af den ikoniske Old Faithful gejser i Gulsten. For hver udbrud har vi målt dens længde og tiden siden den forrige udbrud. Vi antager måske, at der er to “typer” udbrud (rød og gul i diagrammet), og for hver type udbrud genereres de resulterende data ved en (multivariat) normalfordeling. Dette kaldes i øvrigt en Gaussisk Blandingsmodel.

i lighed med k-betyder klyngedannelse starter vi med et tilfældigt gæt for, hvad disse to distributioner / klynger er, og fortsætter derefter med at forbedre iterativt ved at skifte to trin:

1. (forventning) tildel hvert datapunkt til en klynge probabilistisk. I dette tilfælde beregner vi sandsynligheden for, at den kom fra henholdsvis den røde klynge og den gule klynge.
2. (maksimering) Opdater parametrene for hver klynge (vægtet gennemsnitlig placering og varians-kovariansmatrice) baseret på punkterne i klyngen (vægtet efter deres sandsynlighed tildelt i det første trin).

Bemærk, at i modsætning til i k-betyder klyngedannelse, er vores model generativ: den foregiver at fortælle os den proces, hvormed dataene blev genereret. Og vi kunne igen prøve modellen for at generere flere (falske) data.

fik det? Nu skal vi lave et 1-dimensionelt eksempel med ligninger.

overvej datapunkter med en enkelt måling h. vi antager, at disse genereres af 2 klynger hver efter en normalfordeling N(lp, LP2). Sandsynligheden for, at data genereres af den første klynge, er kr.

så vi har 5 parametre: en blanding af sandsynligheden for, og en gennemsnitlig, og standardafvigelsen for hver klynge. Jeg vil betegne dem kollektivt som Kristus.

hvad er sandsynligheden for at observere et datapunkt med værdi? Lad normalfordelingens sandsynlighedsdensitetsfunktion betegnes med kr. For at holde notationen mindre rodet, vil jeg bruge standardafvigelsen som en parameter i stedet for den sædvanlige varians.

sandsynligheden (sandsynligheden) for at observere hele vores datasæt af n punkter er:

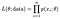
og vi vælger typisk at tage logaritmen af dette for at gøre vores produkt til en mere håndterbar sum, log-sandsynligheden.

vores mål er at maksimere dette: vi ønsker, at vores parametre skal være dem, hvor det mest sandsynligt er, at vi observerer de data, vi observerede (en Estimator for maksimal sandsynlighed).

nu er spørgsmålet, Hvordan skal vi optimere det? At gøre det direkte og analytisk ville være vanskeligt på grund af summen i logaritmen.

tricket er at forestille sig, at der er en latent variabel, som vi vil kalde kr. Det er en binær (0/1-værdsat) variabel, der bestemmer, om et punkt er i klynge 1 eller klynge 2. Hvis vi kender Kurr for hvert punkt, ville det være meget let at beregne estimaterne for maksimal sandsynlighed for vores parametre. For nemheds skyld at matche vores valg af at være 1 For den anden klynge, skifter vi til at være sandsynligheden for, at et punkt er i den anden klynge.

Bemærk, at beløbene nu er uden for logaritmen. Vi henter også et ekstra beløb for at tage højde for sandsynligheden for at observere hver kur.

hvis vi antager kontrafaktisk, at vi observerede kursen, er de maksimale sandsynlighedsestimater lette at danne. For karrus skal du tage prøvegennemsnittet inden for hver klynge; for karrus, ligeledes standardafvigelsen (befolkningsformlen, som er MLE). For Kurt, prøven andel af punkter i den anden klynge. Dette er de sædvanlige estimatorer for maksimal sandsynlighed for hver parameter.

selvfølgelig observerede vi ikke Kurt. Løsningen på dette er hjertet i forventnings-Maksimeringsalgoritmen. Vores plan er:

1. Start med et vilkårligt indledende valg af parametre.
2. (forventning) danner et estimat af kur.
3. (maksimering) Beregn estimatorerne for maksimal sandsynlighed for at opdatere vores parameterestimat.
4. Gentag trin 2 og 3 til konvergens.

igen kan du finde det nyttigt at tænke på k-betyder klyngedannelse, hvor vi gør det samme. I K-betyder klyngedannelse tildeler vi hvert punkt til det nærmeste centroid (forventningstrin). I det væsentlige er dette et hårdt skøn over Kurt. Hårdt, fordi det er 1 for en af klyngerne og 0 for alle de andre. Derefter opdaterer vi centroiderne for at være gennemsnittet af punkterne i klyngen (maksimeringstrin). Dette er den maksimale sandsynlighedsestimator for kr. I k-betyder klyngedannelse har” modellen ” for dataene ikke en standardafvigelse. (“Modellen” er i skræmmende citater, fordi den ikke er generativ).

i vores eksempel, vi vil i stedet gøre en blød opgave af Kurt. Vi kalder dette undertiden ansvaret (hvor ansvarlig er hver klynge for hver observation). Vi vil betegne ansvaret som Kristian.

nu kan vi skrive ned den fulde algoritme til dette eksempel. Men før vi gør det, vil vi hurtigt gennemgå en tabel med symboler, vi har defineret (der var meget).

og her er algoritmen:

Bemærk, at estimaterne af KRP og KRP for klynge 1 er analoge, men bruger 1–KRP som vægtene i stedet.

nu hvor vi har givet et eksempel på algoritmen, har du forhåbentlig en fornemmelse for det. Vi går videre til at diskutere algoritmen generelt. Dette svarer dybest set til at klæde alt, hvad vi gjorde med lidt mere komplicerede variabler. Og det vil sætte os i stand til at forklare, hvorfor det virker.

Forventningsmaksimering generelt

lad os gå videre til den generelle indstilling. Her er opsætningen:

1. vi har nogle data af enhver form.
2. vi postulerer, at der også er uobserverede (latente) data, igen uanset form.
3. vi har en model med parametre LR.
4. vi har evnen til at beregne log-sandsynligheden for, at der er tale om en log-Sandsynlighed for, at der er tale om en log-Sandsynlighed for, at der er tale om en log-Sandsynlighed for, at der er tale om en log-Sandsynlighed. Specifikt log over sandsynligheden for at observere vores data og specificerede opgaver af de latente variabler givet parametrene.
5. vi har også mulighed for at bruge modellen til at beregne den betingede fordeling pr. Vi vil betegne denne P (LP / H; lp).
6. derfor kan vi beregne logsandsynligheden. Dette er loggen over sandsynligheden for at observere vores data givet parametrene (uden at påtage sig en opgave for de latente variabler).

brug af P til at angive sandsynligheden, vi kan nu bruge kædereglen til at skrive:

notationen kan være subtil her. Alle tre udtryk tager parametrene Kurt som en given.

1. det første udtryk til venstre er sandsynligheden for at observere dataene og en specificeret latent variabel tildeling.
2. det første udtryk på højre side er sandsynligheden for den specificerede tildeling af de latente variabler givet de observerede data.
3. det sidste udtryk er sandsynligheden for at observere dataene.

vi kan tage logaritmer og omarrangere vilkår. Så i den anden linje vil vi lave en notationsændring (og en forvirrende ved det. Bebrejd mig ikke, jeg opfandt det ikke):

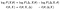
For de to første udtryk er det værd at gennemgå, hvad de er i sammenhæng med vores tidligere eksempel. Den første er den, vi ønsker at optimere. Den anden var den, der var analytisk tractable.

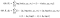
husk nu, at jeg sagde, at vi kan beregne den betingede fordeling i forhold til parametrene? Det er her, tingene bliver vilde.

vi skal introducere et andet sæt af de samme parametre, kalder det til det samme. Jeg vil også nogle gange betegne det med en hat (omkreds) over det, som den, som denne “krig” har.2 Tænk på dette sæt parametre som vores nuværende skøn. Den i øjeblikket i vores formler vil blive optimeret til at forbedre vores estimat.

nu skal vi tage forventningen om logens sandsynligheder med hensyn til den betingede fordeling af vores latente variabler givet dataene og vores nuværende parameterestimat.

udtrykket på venstre side ændres ikke, da det alligevel ikke kender/bryr sig om prise (det er en konstant). Igen er forventningen over de mulige værdier af Kristus. Hvis du følger med i forhold til vores eksempel, ændres udtrykket karrusel(karrusel), efter at vi har taget forventningen, så karrusel erstattes af karrusel.

nu, meget hurtigt, for at forbedre det notationelle mareridt, vi har foregået her, lad os introducere stenografisk notation for de to forventninger, vi har på højre side

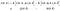
algoritmen bliver:

hvorfor det virker

den tunge løft for at bevise, at dette vil fungere, er at overveje funktionen r(kr, kr). Påstanden er, at R maksimeres, når lp=lp. I stedet for en fuld bevis lad os tænke over, hvad R beregner. Når vi fjerner afhængigheden af dataene (som deles mellem den fordeling, vi tager en forventning over, og sandsynlighedsfunktionen), bliver R skematisk

med andre ord har vi to sandsynlighedsfordelinger. Vi bruger den ene (parametreret af prisT) til at generere data, og vi bruger den anden (parametreret af prisT) til at beregne sandsynligheden for det, vi så. Hvis prisT repræsenterer kun et enkelt tal, og fordelingerne har sandsynlighedsdensitetsfunktioner, kunne vi skrive (igen skematisk)

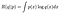
jeg har suggestivt skrevet dette i en form svarende til Kullback-Leibler (KL) divergens, som er (næsten) et mål for afstanden mellem to sandsynlighedsfordelinger. Hvis vi trækker R(K||p) fra en konstant R(p||p), får vi KL-divergensen, der er afgrænset nedenfor ved 0 og kun er 0, når k=s. (det eneste en afstand3 0 fra fordelingen p er p selv). Dette er et standardresultat om KL-divergensen og kan bevises med Jensens ulighed.4946 >

nu er det eneste, der er tilbage at gøre, at overveje forskellen mellem sandsynligheden før og efter vores opdateringstrin:

vi valgte de nye parametre for at maksimere spørgsmål, så den første periode er bestemt positiv. Ved argumentet ovenfor maksimeres R ved at tage de gamle parametre som sit første argument, så det andet udtryk skal være negativt. Positiv minus negativ er positiv. Derfor er sandsynligheden steget ved hvert opdateringstrin. Hvert trin er garanteret at gøre tingene bedre.

Bemærk også, at vi ikke behøver at optimere K. Alt, hvad vi skal, er at finde en måde at gøre det bedre på, og vores opdateringer er stadig garanteret at gøre tingene bedre.

konklusion

forhåbentlig har du nu en god fornemmelse for algoritmen. Med hensyn til matematik er nøgleligningen bare sandsynligheden nedenfor. Derefter tager vi bare forventninger med hensyn til de gamle parametre (forventningstrinnet) og viser, at vi har det fint med bare at optimere den første periode på højre side. Som vi motiverede med det gaussiske Blandingsmodeleksempel, er dette andet udtryk ofte lettere at optimere. Den tredje periode, vi ikke behøver at bekymre os om, det vil ikke ødelægge noget.

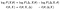
når jeg træder lidt tilbage, vil jeg understrege kraften og nytten af EM-algoritmen. Først og fremmest repræsenterer det ideen om, at vi kan introducere latente variabler og derefter beregne ved skiftevis at håndtere de latente variabler (tage parametrene som faste og kendte) og håndtere parametrene (tage de latente variabler som faste og kendte). Dette er en stærk ide, som du vil se i forskellige sammenhænge.

for det andet er algoritmen iboende hurtig, fordi den ikke afhænger af computergradienter. Når som helst du kan løse en model analytisk (som at bruge en lineær regression), bliver det hurtigere. Og dette lader os tage analytisk uhåndterlige problemer og løse dele af dem analytisk og udvide denne magt til en iterativ kontekst.

endelig vil jeg bemærke, at der er meget mere at sige om EM-algoritmen. Det generaliseres til andre former for maksimeringstrin og til variationsbyesiske teknikker og kan forstås på forskellige måder (for eksempel som maksimering-maksimering eller som skiftende fremskrivninger til en submanifold under gensidigt dobbelt affine forbindelser på en statistisk manifold (e – og m – forbindelserne)). Mere om det i fremtiden!