maximizarea așteptărilor explicată

maximizarea așteptărilor (EM) este un algoritm clasic dezvoltat în anii 60 și 70 cu aplicații diverse. Acesta poate fi folosit ca un algoritm de clustering nesupravegheat și se extinde la aplicații NLP, cum ar fi alocarea latentă Dirichlet1, algoritmul Baum–Welch pentru modelele Markov ascunse și imagistica medicală. Ca procedură de optimizare, este o alternativă la coborârea gradientului și altele asemenea, cu avantajul major că, în multe circumstanțe, actualizările pot fi calculate analitic. Mai mult decât atât, este un cadru flexibil pentru gândirea la optimizare.

în acest articol, vom începe cu un exemplu simplu de grupare și apoi vom discuta algoritmul în generalitate.

luați în considerare situația în care aveți o varietate de puncte de date cu unele măsurători ale acestora. Dorim să le atribuim diferitelor grupuri.

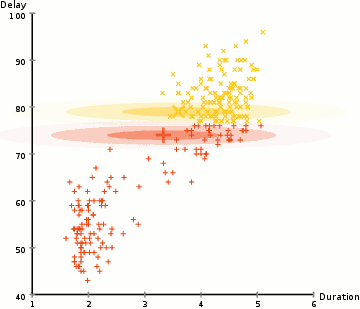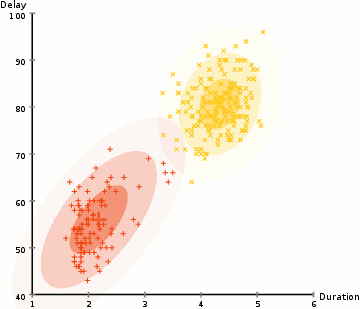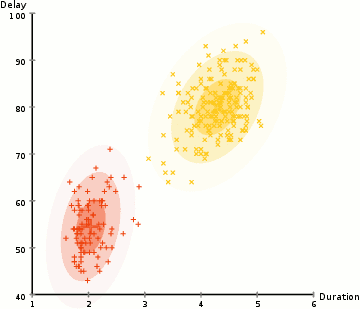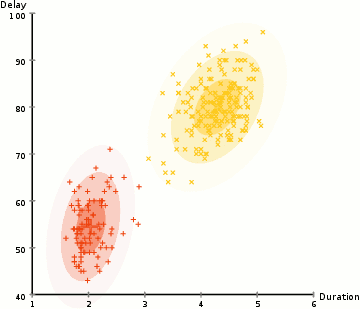
în exemplul de aici avem date despre erupțiile gheizerului iconic Old Faithful din Yellowstone. Pentru fiecare Erupție, am măsurat lungimea și timpul de la erupția anterioară. Am putea presupune că există două „tipuri” de erupții (roșu și galben în diagramă), iar pentru fiecare tip de Erupție datele rezultate sunt generate de o distribuție normală (multivariată). Aceasta se numește un model de amestec Gaussian, întâmplător.

Similar cu K-înseamnă clustering, vom începe cu o presupunere aleatoare pentru ceea ce aceste două distribuții / clustere sunt și apoi trece la îmbunătățirea iterativ prin alternarea doi pași:

1. (așteptare) atribuiți fiecare punct de date unui cluster probabilistic. În acest caz, calculăm probabilitatea provenită din clusterul roșu și respectiv clusterul galben.
2. (maximizare) actualizați parametrii pentru fiecare cluster (locația medie ponderată și matricea varianță-covarianță) pe baza punctelor din cluster (ponderate de probabilitatea lor atribuită în primul pas).

rețineți că, spre deosebire de K-înseamnă clustering, modelul nostru este generativ: pretinde să ne spună procesul prin care au fost generate datele. Și am putea, la rândul său, să re-eșantionăm modelul pentru a genera mai multe date (false).

ai înțeles? Acum vom face un exemplu 1-dimensional cu ecuații.

luați în considerare punctele de date cu o singură măsurătoare x. presupunem că acestea sunt generate de 2 clustere, fiecare urmând o distribuție normală N(in. Probabilitatea ca datele să fie generate de primul cluster este egală cu a.

deci avem 5 parametri: o probabilitate de amestecare a valorilor de la 0 la sută, precum și o medie a valorilor de la 0 la sută și o medie a deviației standard de la zero pentru fiecare grup. Le voi desemna în mod colectiv ca fiind de la egal la egal.

care este probabilitatea de a observa un punct de date cu valoarea x? Fie ca funcția de probabilitate-densitate a distribuției normale să fie notată cu Ecuator. Pentru a păstra notația mai puțin aglomerată, voi folosi abaterea standard ca parametru în loc de varianța obișnuită.

probabilitatea (probabilitatea) de a observa întregul nostru set de date de n puncte este:

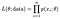
și de obicei alegem să luăm logaritmul acestui lucru pentru a transforma produsul nostru într-o sumă mai ușor de gestionat, log-probabilitatea.

scopul nostru este de a maximiza acest lucru: dorim ca parametrii noștri să fie cei în care este cel mai probabil să observăm datele pe care le-am observat (un Estimator de probabilitate maximă).

acum întrebarea este, cum o vom optimiza? A face acest lucru direct și analitic ar fi dificil din cauza sumei din logaritm.

trucul este sa ne imaginam ca exista o variabila latenta pe care o vom numi inox. Este o variabilă binară (cu valoare 0/1) care determină dacă un punct este în cluster 1 sau cluster 2. Dacă știm că pentru fiecare punct, ar fi foarte ușor să calculăm estimările de probabilitate maximă ale parametrilor noștri. Pentru comoditate, pentru a se potrivi cu alegerea noastră de a fi 1 Pentru al doilea cluster, vom schimba pentru a fi probabilitatea ca un punct să fie în al doilea cluster.

observați că sumele sunt acum în afara logaritmului. De asemenea, vom ridica o sumă suplimentară pentru a ține cont de probabilitatea de a observa fiecare hectar.

presupunând, în mod contrafactual, că am observat, că estimările probabilității maxime sunt ușor de format. Pentru SEC, se ia media eșantionului în cadrul fiecărui grup; pentru SEC, de asemenea, deviația standard (formula populației, care este MLE). Pentru sec, proporția eșantionului de puncte din cel de-al doilea cluster. Acestea sunt estimatorii uzuali de probabilitate maximă pentru fiecare parametru.

desigur, nu am observat un număr de la un număr de la un număr de la un număr de la un număr de la un număr de la altul. Soluția la aceasta este inima algoritmului de așteptare-maximizare. Planul nostru este:

1. începeți cu o alegere inițială arbitrară a parametrilor.
2. (așteptare) formează o estimare a valorii de la 7XT.
3. (maximizare) calculați estimatorii de probabilitate maximă pentru a actualiza estimarea parametrilor noștri.
4. repetați pașii 2 și 3 pentru convergență.

din nou, s-ar putea să vă fie util să vă gândiți la gruparea K-înseamnă, unde facem același lucru. În K-înseamnă clustering, atribuim fiecare punct celui mai apropiat centroid (etapa de așteptare). In esenta, aceasta este o estimare greu de Centenar. Greu pentru că este 1 pentru unul dintre clustere și 0 pentru toate celelalte. Apoi actualizăm centroizii pentru a fi media punctelor din cluster (pasul de maximizare). Acesta este Estimatorul probabilității maxime pentru cifra de afaceri. În K-înseamnă clustering,” modelul ” pentru date nu are o abatere standard. („Modelul” este în citate speriate, deoarece nu este generativ).

în exemplul nostru, vom face în schimb o atribuire ușoară a lui XV. Uneori numim aceasta responsabilitate (cât de responsabil este fiecare grup pentru fiecare observație). Vom denota responsabilitatea ca fiind de ordinul al VIII-lea.

acum putem scrie algoritmul complet pentru acest exemplu. Dar înainte de a face acest lucru, vom revizui rapid un tabel de simboluri pe care le-am definit (au existat multe).

și aici este algoritmul:

rețineți că estimările de la centimetrele 1 și de la centimetrele 1 sunt similare, dar folosind în schimb 1–centimetrele ca ponderi.

acum că am dat un exemplu de algoritm, sperăm că aveți o senzație pentru el. Vom trece la discutarea algoritmului în general. Acest lucru se ridică practic la îmbrăcarea a tot ceea ce am făcut cu variabile puțin mai complicate. Și ne va pune în poziția de a explica de ce funcționează.

maximizarea așteptărilor în General

să trecem la setarea generală. Aici este configurarea:

1. avem niște date X de orice formă.
2. afirmăm că există, de asemenea, date neobservate (latente), din nou, de orice formă.
3. avem un model cu parametrii de la ora actuală.
4. avem capacitatea de a calcula log-probability-ul(X, X, X). Mai exact, Jurnalul probabilității de a observa datele noastre și atribuirile specificate ale variabilelor latente date parametrilor.
5. avem, de asemenea, capacitatea de a utiliza modelul pentru a calcula distribuția condiționată a modelului, având în vedere un set de parametri. Vom denumi acest P (XV/ X; XV).
6. în consecință, putem calcula log-probability-ul(X). Acesta este jurnalul probabilității de a observa datele noastre date parametrilor (fără a presupune o atribuire pentru variabilele latente).

folosind P pentru a indica probabilitatea, putem folosi acum regula lanțului pentru a scrie:

notația poate fi subtilă aici. Toți cei trei termeni iau parametrii ca fiind dat.

1. primul termen din stânga este probabilitatea de a observa datele și o atribuire variabilă latentă specificată.
2. primul termen din partea dreaptă este probabilitatea atribuirii specificate a variabilelor latente date datelor observate.
3. ultimul termen este probabilitatea de a observa datele.

putem lua logaritmi și rearanja Termeni. Apoi, în a doua linie vom face o schimbare de notație (și una confuză la asta. Nu da vina pe mine, nu am inventat-o):

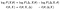
pentru primii doi termeni, merită revizuită ceea ce sunt în contextul exemplului nostru anterior. Primul, cel de-al doilea, este cel pe care dorim să-l optimizăm. Cea de-a doua, ℓ(θ; X, Δ), a fost cel care a fost analitic maleabil.

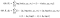
acum, amintiți-vă că am spus că putem calcula distribuția condiționată a Ecuatorului|X, având în vedere parametrii ecuatorului? Acest lucru este în cazul în care lucrurile devin sălbatice.

vom introduce un al doilea set de aceiași parametri, numiți-l la fel. De asemenea, o voi denota uneori cu o pălărie (circumflex) peste ea, ca cea pe care o are acest „inextricabil”.2 gândiți-vă la acest set de parametri ca la estimarea noastră actuală. În prezent, în formulele noastre va fi optimizat pentru a îmbunătăți estimarea noastră.

acum vom lua așteptarea probabilităților jurnalului în ceea ce privește distribuția condițională a numerelor de serie, respectiv distribuția variabilelor noastre latente, având în vedere datele și estimarea actuală a parametrilor.

termenul de pe partea stângă nu se schimbă, deoarece nu știe/pasă de Oricum (este o constantă). Din nou, așteptarea este peste valorile posibile ale lui sec. Dacă sunteți în urma de-a lungul cu privire la exemplul nostru, termenul ℓ(θ; X, Δ) se modifică după așteptările, astfel încât Δ se înlocuiește cu ɣ.

acum, foarte repede, pentru a ameliora coșmarul notațional pe care îl avem aici, să introducem notația stenografică pentru cele două așteptări pe care le avem în partea dreaptă

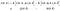
algoritmul devine:

de ce funcționează

ridicarea grea pentru a dovedi că acest lucru va funcționa este de a lua în considerare funcția R(inkt. Afirmația este că R este maximizată atunci când XL = XL. În locul unei dovezi complete, să ne gândim la ceea ce calculează R. Îndepărtând dependența de datele X (care este împărțită între distribuția pe care o luăm o așteptare și funcția de probabilitate), r devine schematic

cu alte cuvinte, avem două distribuții de probabilitate. Noi folosim unul (parametrizat prin Ecuador) pentru a genera date, iar celălalt (parametrizat prin Ecuador) pentru a calcula probabilitatea a ceea ce am văzut. Dacă un singur număr reprezintă un singur număr, iar distribuțiile au funcții de densitate de probabilitate, am putea scrie (din nou, schematic)

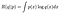
am scris sugestiv acest lucru într-o formă similară cu cea a divergenței Kullback-Leibler (KL) care este (aproape) o măsură a distanței dintre două distribuții de probabilitate. Dacă scădem R(q||p) dintr-o constantă R (p||p) vom obține KL-divergența care este delimitată mai jos la 0 și este doar 0 când q=p. (singurul lucru o distanță3 0 din distribuția p este p în sine). Cu alte cuvinte, R este maximizat atunci când q=p. acesta este un rezultat standard despre KL-divergență și poate fi dovedit cu inegalitatea lui Jensen.^

acum, singurul lucru rămas de făcut este să luăm în considerare diferența dintre probabilitățile înainte și după pasul nostru de actualizare:

am ales noii parametri pentru a maximiza Q, astfel încât primul termen este cu siguranță pozitiv. Prin argumentul de mai sus, R este maximizat luând parametrii vechi ca prim argument, deci al doilea termen trebuie să fie negativ. Pozitiv minus negativ este pozitiv. Prin urmare, probabilitatea a crescut la fiecare pas de actualizare. Fiecare pas este garantat pentru a face lucrurile mai bune.

observați, de asemenea, că nu trebuie să optimizăm Q. Tot ce trebuie să găsim este o modalitate de a face mai bine și actualizările noastre sunt încă garantate pentru a face lucrurile mai bine.

concluzie

sperăm că acum aveți o senzație bună pentru algoritm. În ceea ce privește matematica, ecuația cheie este doar probabilitatea de mai jos. După aceea, luăm doar așteptări cu privire la parametrii vechi (pasul de așteptare) și arătăm că suntem bine să optimizăm doar primul termen din partea dreaptă. Așa cum am motivat cu exemplul modelului de amestec Gaussian, acest al doilea termen este adesea mai ușor de optimizat. Al treilea termen de care nu trebuie să ne facem griji, nu va strica nimic.

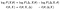
trecând puțin înapoi, vreau să subliniez puterea și utilitatea algoritmului EM. În primul rând, reprezintă ideea că putem introduce variabile latente și apoi să calculăm tratând alternativ variabilele latente (luând parametrii ca fix și cunoscut) și tratând parametrii (luând variabilele latente ca fixe și cunoscute). Aceasta este o idee puternică pe care o veți vedea într-o varietate de contexte.

în al doilea rând, algoritmul este inerent rapid, deoarece nu depinde de gradienții de calcul. Oricând puteți rezolva un model analitic (cum ar fi utilizarea unei regresii liniare), va fi mai rapid. Și asta ne permite să luăm probleme greu de rezolvat din punct de vedere analitic și să rezolvăm părți din ele în mod analitic, extinzând acea putere într-un context iterativ.

în cele din urmă, vreau să notez că mai sunt multe de spus despre algoritmul EM. Se generalizează la alte forme de realizare a etapei de maximizare și la tehnici Bayesiene variaționale și poate fi înțeleasă în moduri diferite (de exemplu ca maximizare-maximizare sau ca proiecții alternante la un submanifold sub conexiuni afine reciproc duale pe o varietate statistică (conexiunile e – și m)). Mai multe despre asta în viitor!