Forventning Maksimering Forklart

Forventningsmaksimering (EM) er en klassisk algoritme utviklet på 60-og 70-tallet med ulike applikasjoner. Den kan brukes som en uovervåket klyngealgoritme og strekker SEG TIL nlp-applikasjoner Som Latent Dirichlet-Tildeling1, baum-Welch-algoritmen For Skjulte Markov-Modeller og medisinsk bildebehandling. Som en optimaliseringsprosedyre er det et alternativ til gradient nedstigning og lignende med den store fordelen at oppdateringene i mange tilfeller kan beregnes analytisk. Mer enn det er det et fleksibelt rammeverk for å tenke på optimalisering.

i denne artikkelen starter vi med et enkelt klyngeeksempel og diskuterer algoritmen generelt.

Vurder situasjonen der du har en rekke datapunkter med noen målinger av dem. Vi ønsker å tildele dem til ulike grupper.

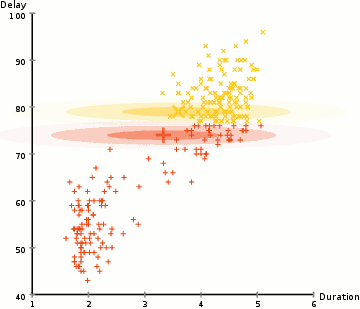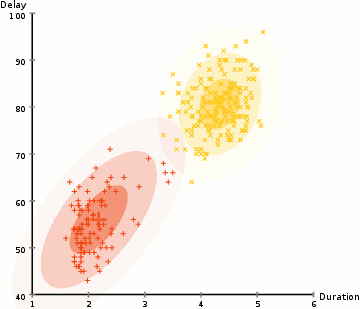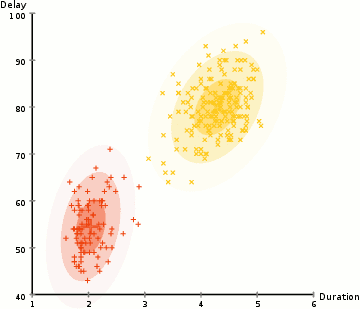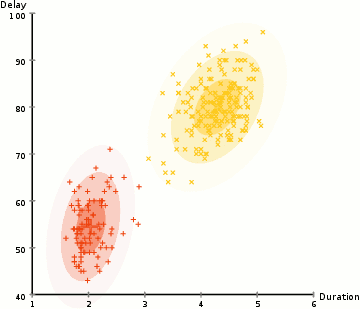
i eksemplet her har vi data om utbrudd av den ikoniske Old Faithful geysir i Yellowstone. For hvert utbrudd har vi målt lengden og tiden siden forrige utbrudd. Vi kan anta at det er to» typer » utbrudd (rød og gul i diagrammet), og for hver type utbrudd genereres de resulterende dataene ved En (multivariat) Normalfordeling. Dette kalles en Gaussisk Blandingsmodell, forresten.

I Likhet med k-means clustering, starter vi med en tilfeldig gjetning for hva de to distribusjonene / klyngene er, og fortsetter deretter å forbedre iterativt ved å skifte to trinn:

1. (Forventning) Tilordne hvert datapunkt til en klynge probabilistisk. I dette tilfellet beregner vi sannsynligheten for at den kom fra henholdsvis den røde klyngen og den gule klyngen.
2. (Maksimering) Oppdater parametrene for hver klynge (vektet gjennomsnittlig plassering og varians-kovariansmatrise) basert på punktene i klyngen (vektet av sannsynligheten tildelt i første trinn).

Merk at i motsetning til i k-means clustering, er vår modell generativ: den har til hensikt å fortelle oss prosessen der dataene ble generert. Og vi kunne i sin tur prøve modellen på nytt for å generere flere (falske) data.

Har du det? Nå skal vi gjøre et 1-dimensjonalt eksempel med ligninger.

Vurder datapunkter med en enkelt måling x. vi antar at disse genereres av 2 klynger hver etter en normal fordeling N(μ, σ2). Sannsynligheten for at data genereres av den første klyngen er π.

så vi har 5 parametere: en blandingssannsynlighet π, og en gjennomsnittlig μ og standardavvik σ for hver klynge. Jeg vil betegne dem kollektivt som θ.

hva er sannsynligheten for å observere et datapunkt med verdi x? La normalfordelingens sannsynlighetstetthetsfunksjon betegnes med ϕ. For å holde notasjonen mindre rotete, vil jeg bruke standardavviket som en parameter i stedet for den vanlige variansen.

sannsynligheten (sannsynligheten)for å observere hele vårt datasett av n poeng er:

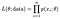
og vi velger vanligvis å ta logaritmen til dette for å gjøre produktet vårt til en mer håndterlig sum, log-sannsynligheten.

vårt mål er å maksimere dette: vi vil at våre parametere skal være de der det er mest sannsynlig at vi observerer dataene vi observerte (En Maksimal Sannsynlighets Estimator).

nå er spørsmålet, hvordan skal vi optimalisere det? Å gjøre det direkte og analytisk ville være vanskelig på grunn av summen i logaritmen.

trikset er å forestille seg at det er en latent variabel som vi vil kalle Δ. Det er en binær (0/1-verdi) variabel som bestemmer om et punkt er i klynge 1 eller klynge 2. Hvis vi vet Δ for hvert punkt, vil det være veldig enkelt å beregne maksimumsannsynlighets-estimatene for parametrene våre. For å gjøre det lettere for Oss å matche Vårt valg av Δ som 1 for den andre klyngen, vil vi bytte π til å være sannsynligheten for at et punkt er i den andre klyngen.

legg Merke til at summene nå er utenfor logaritmen. Vi henter også en ekstra sum for å ta hensyn til sannsynligheten for å observere hver Δ.

Hvis vi Antar at vi motvirket At Vi observerte Δ, er de maksimale sannsynlighetsestimatene enkle å danne. For μ, ta utvalgsgjennomsnittet innenfor hver klynge; for σ, på samme måte standardavviket(populasjonsformelen, SOM ER MLE). For π er utvalgsandelen av poeng i den andre klyngen. Dette er de vanlige estimatene for maksimal sannsynlighet for hver parameter.

Vi observerte Selvfølgelig Ikke Δ. Løsningen på dette er hjertet Av Forventnings-Maksimeringsalgoritmen. Vår plan er:

1. Start med et vilkårlig innledende valg av parametere.
2. (Forventning) Danner et estimat Av Δ.
3. (Maksimering) Beregn estimatene for maksimal sannsynlighet for å oppdatere parameterestimatet.
4. Gjenta trinn 2 og 3 til konvergens.

Igjen, du kan finne det nyttig å tenke på k-means clustering, hvor vi gjør det samme. I k-betyr clustering tilordner vi hvert punkt til nærmeste sentroid (forventningstrinn). I hovedsak er dette et hardt estimat av Δ. Vanskelig fordi det er 1 for en av klyngene og 0 for alle de andre. Da oppdaterer vi sentroidene for å være gjennomsnittet av punktene i klyngen (maksimeringstrinn). Dette er estimatoren for maksimumsannsynlighet for μ. I k-betyr clustering har» modellen » for dataene ikke et standardavvik. («Modellen» er i skremme sitater fordi den ikke er generativ).

i vårt eksempel vil vi i stedet gjøre en myk tildeling av Δ. Vi kaller dette noen ganger ansvaret (hvor ansvarlig er hver klynge for hver observasjon). Vi vil betegne ansvaret som ɣ.

nå kan vi skrive ned hele algoritmen for dette eksemplet. Men før vi gjør det, vil vi raskt gjennomgå et bord med symboler vi har definert (det var mye).

og her er algoritmen:

Merk at estimatene for μ og σ for klynge 1 er analoge, men bruker i stedet 1–ɣ som vekter.

Nå som vi har gitt et eksempel på algoritmen, har du forhåpentligvis en følelse for det. Vi fortsetter å diskutere algoritmen generelt. Dette utgjør i utgangspunktet å kle opp alt vi gjorde med litt mer kompliserte variabler. Og det vil sette oss i stand til å forklare hvorfor det fungerer.

Forventningsmaksimering Generelt

la oss gå til den generelle innstillingen. Her er oppsettet:

1. Vi har noen data X uansett form.
2. vi sier at det også er uobserverte (latente) data Δ, igjen uansett form.
3. vi har en modell med parametere θ.
4. Vi har muligheten til å beregne loggsannsynlighet ℓ(θ; X, Δ). Spesielt loggen av sannsynligheten for å observere våre data og spesifiserte oppdrag av latente variabler gitt parametrene.
5. vi har også muligheten til å bruke modellen til å beregne Betinget distribusjon Δ / X gitt et sett med parametere. Vi vil betegne Denne P(Δ/ X; θ).
6. Derfor kan vi beregne log-sannsynligheten ℓ(θ; X). Dette er loggen av sannsynligheten for å observere våre data gitt parametrene (uten å anta en oppgave for latente variabler).

Ved Å bruke P for å betegne sannsynligheten, kan vi nå bruke kjederegelen til å skrive:

notasjonen kan være subtil her. Alle tre begrepene tar parameterne θ som en gitt.

1. den første termen til venstre er sannsynligheten for å observere dataene og en spesifisert latent variabel tildeling.
2. den første termen på høyre side er sannsynligheten for den angitte tildelingen av latente variabler gitt de observerte dataene.
3. siste term er sannsynligheten for å observere dataene.

Vi kan ta logaritmer og omorganisere vilkår. Så i den andre linjen vil vi gjøre en notasjonsendring (og en forvirrende en på det. Ikke klandre meg, jeg fant ikke opp det):

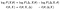
For de to første begrepene er det verdt å vurdere hva de er i sammenheng med vårt tidligere eksempel. Den første, ℓ (x), er den vi ønsker å optimalisere. For det andre, ℓ(x, Δ), var det en som var analytisk medgjørlig.

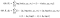
nå, husk at jeg sa at vi kan beregne den betingede distribusjonen Δ / X gitt parametrene θ? Det er her ting blir vilt.

vi skal introdusere et annet sett med de samme parametrene, kall det θʹ. Jeg vil også noen ganger betegne den med en lue (circumflex) over den, som den denne » ê » har.2 Tenk på dette settet av parametere som vårt nåværende estimat. Den θ som for øyeblikket er i formlene våre, vil bli optimalisert for å forbedre vårt estimat.

nå skal vi ta forventningen om loggens sannsynligheter med hensyn til den betingede distribusjonen Δ|X, θʹ – nemlig fordelingen av våre latente variabler gitt dataene og vårt nåværende parameterestimat.

begrepet på venstre side endres ikke siden det ikke vet/bryr seg om Δ uansett (det er en konstant). Igjen er forventningen over de mulige verdiene Til Δ. Hvis du følger sammen med hensyn til vårt eksempel, endres termen ℓ(θ; X, Δ) etter at Vi har valgt en forventning om At Δ erstattes av ɣ.

nå, veldig raskt, for å forbedre notasjonsmarerittet vi har her, la oss introdusere shorthand notasjon for de to forventningene vi har på høyre side

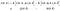
algoritmen blir:

Hvorfor Det Fungerer

den tunge løftingen for å bevise at dette vil fungere, er å vurdere funksjonen R (θ, θʹ). Kravet er At r maksimeres når θ=θʹ. I stedet for et fullstendig bevis, la oss tenke på Hva R beregner. Stripping bort avhengigheten Av dataene X (som deles mellom fordelingen vi tar en forventning over og sannsynlighetsfunksjonen), blir r skjematisk

med andre ord har vi to sannsynlighetsfordelinger. Vi bruker den ene (parameterisert av θʹ) til å generere data δ, og vi bruker den andre (parameterisert av θ) til å beregne sannsynligheten for det vi så. Hvis Δ representerer bare et enkelt tall og fordelingene har sannsynlighetstetthetsfunksjoner, kan vi skrive (igjen, skjematisk)

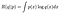
jeg har suggestivt skrevet dette i en form som ligner På Kullback-Leibler (KL) Divergensen som er (nesten) et mål på avstanden mellom to sannsynlighetsfordelinger. Hvis vi trekker R (q / / p) fra en konstant R (p / / p), får VI kl-divergensen som er begrenset under 0 og er bare 0 når q = p. (det eneste en avstand3 0 fra fordelingen p er p selv). Med Andre ord maksimeres R når q = p. Dette er et standardresultat om kl-divergensen og kan bevises Med Jensens ulikhet.④

nå er det eneste som gjenstår å gjøre, å vurdere forskjellen mellom sannsynligheten før og etter oppdateringstrinnet vårt:

vi valgte de nye parametrene for å maksimere Q, så den første termen er definitivt positiv. Ved argumentet ovenfor maksimeres R ved å ta de gamle parametrene som sitt første argument, så den andre termen må være negativ. Positiv minus negativ er positiv. Derfor har sannsynligheten økt ved hvert oppdateringstrinn. Hvert trinn er garantert å gjøre ting bedre.

Legg Også Merke til at Vi ikke trenger å optimalisere Q. Alt vi trenger er å finne noen måte å gjøre det bedre og våre oppdateringer er fortsatt garantert å gjøre ting bedre.

Konklusjon

Forhåpentligvis har du nå en god følelse for algoritmen. Når det gjelder matematikken, er nøkkelligningen bare sannsynligheten nedenfor. Etter det tar vi bare forventninger med hensyn til de gamle parametrene (forventningstrinnet) og viser at vi har det bra å bare optimalisere første sikt på høyre side. Som vi motiverte Med Det Gaussiske Blandingsmodelleksemplet, er denne andre termen ofte lettere å optimalisere. Den tredje termen vi ikke trenger å bekymre oss for, det vil ikke ødelegge noe.

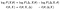
Stepping tilbake litt, jeg vil understreke kraften OG nytten AV em-algoritmen. Først av alt representerer det ideen om at vi kan introdusere latente variabler og deretter beregne ved vekselvis å håndtere de latente variablene (ta parametrene som fast og kjent) og håndtere parametrene (ta de latente variablene som fast og kjent). Dette er en kraftig ide som du vil se i en rekke sammenhenger.

For Det Andre er algoritmen iboende rask fordi den ikke er avhengig av beregningsgradienter. Når som helst du kan løse en modell analytisk (som å bruke en lineær regresjon), blir det raskere. Og dette lar oss ta analytisk vanskelige problemer og løse deler av dem analytisk, og utvide den kraften til en iterativ kontekst.

Til Slutt vil Jeg merke at DET er mye mer å si OM EM-algoritmen. Det generaliserer til andre former for å gjøre maksimeringstrinnet og til variasjonelle Bayesianske teknikker og kan forstås på forskjellige måter (for eksempel som maksimering-maksimering eller som alternerende fremspring til en submanifold under gjensidig doble affinforbindelser på en statistisk manifold (e – og m – forbindelsene)). Mer om det i fremtiden!